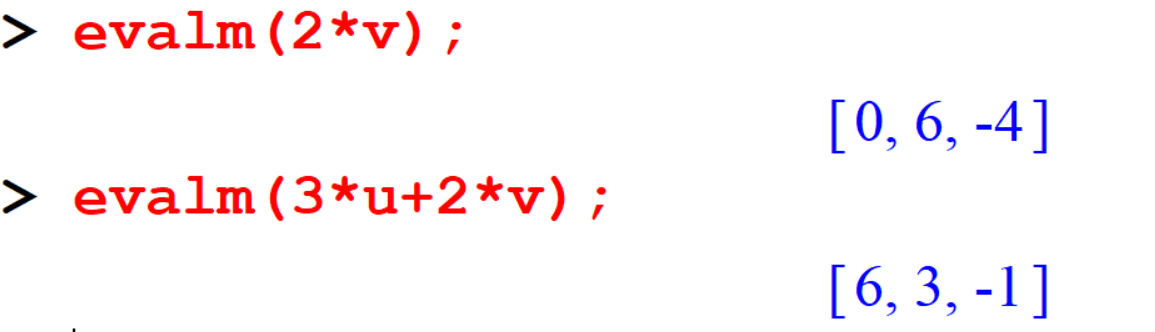Lesson 5 Vectors
5.1 Defining a vector
A vector in Maple is a one-dimensional array. It is part of the linalg package. There are two commands for entering a vector in Maple. Those are array and vector.
[> with(linalg):
[> u:=array([a,b,c]);
[> v:=vector([a,b,c]);
[> w:=<a|b|c>; 
Defining a vector with specified elements:
[> a:=vector([1,2,3]);
[> b:=vector(3,[-1,2,3]);
Defining a vector with 3 unspecified elements will gives you a symbolic vector of dimension three.
[> c:=vector(3);
[> evalm(c); 
[> u:=vector([3,-2,0,2,-3]); 
If a vector u is defined, we can access the \(n\)th element of the vector u by the command u[n].

We can insert variables as the entries of vectors:
[> v := vector([x,y,2*x]);
[> v[1]+v[3]^2; 
Given below is the function form of the “vector” command.
[> w := vector(7, i -> i^2-1);
This \(w\) vector contains the \(n^2-1\) form of the first seven positive integers. \(n \in \mathbb{N}\).
5.2 Vector Algebra
Maple can handle most of the common operations with vectors.
5.2.1 Vector addition
The commonly used algebra operations on vectors are as follows:
[> u:=vector([2,-1,1]);
[> v:=vector([0,3,-2]);
[> u+v; 
Notice that just typing \(u+v\) doesn’t work the way you expect. To see the entries you need to use evalm which stands for Evaluate as a Matrix. So now:
> evalm(u+v);
> evalm(u-v); 
5.2.3 Dot product and cross product
To do the dot and cross products, you have the commands dotprod and crossprod. But you must load the linalg package before entering those commands.
But you must load the ‘linalg’ package before entering those commands.
[> with(linalg):
[> dotprod(u,v);
[> crossprod(u,v); 
[> crossprod([1,2,3],[-2,0,1]); 
5.2.4 Scalar triple product
There are two methods to get the scalar triple product.
[> u:=vector([3,-1,2]);
[> v:=vector([5,7,1]);
[> w:=vector([0,1,2]);- Method I
dotprod(u,crossprod(v,w)); - Method II
det(augment(u,v,w)); 
5.2.5 Magnitude of a vector
- Method I
[> u:=vector([2,-1,1]);
[> sqrt(dotprod(u,u));
[> sqrt(dotprod(v,v));
- Method II
> norm(v,2);
> norm(v,2); 
Using the norm command you can find the unit vector corresponding to a given vector.
[> u/norm(u,2);
[> evalm(%);
[> evalm(v/norm(v,2));
5.2.6 Angle between two vectors
[> angle(u,v);
[> evalf(%);
Note that, in here the angle is given in radians.
5.2.7 Line joining two points and mid point of line
Let \(p,q\) be two position vectors. Then you can find the vector representing the line joining these two points by evaluating \(q-p\).
[> p:=vector([3,-1,2]);
[> q:=vector([5,7,1]);
[> evalm(q-p); 
You can find the midpoint of the line as well.
[> evalm((q+p)/2); 
5.3 Geometrical representation of vectors
Vectors are determined by both a magnitude and a direction and they are represented geometrically in 2 or 3 dimensional space as directed line segments or arrows. We can represent vectors graphically using the arrow and display commands from the plots package.
[> restart;with(plots): The arrow command has the following format:
arrow(vector,options) or arrow(base,direction,options)
For the options, you may use a bigger width if the arrow appears to be too small.
For example, in 2-dimensional plane plot the vector \(\vec u=(3,5)\)
> arrow([3,5],width=0.1,head_length=0.5,axes=normal,color=red); 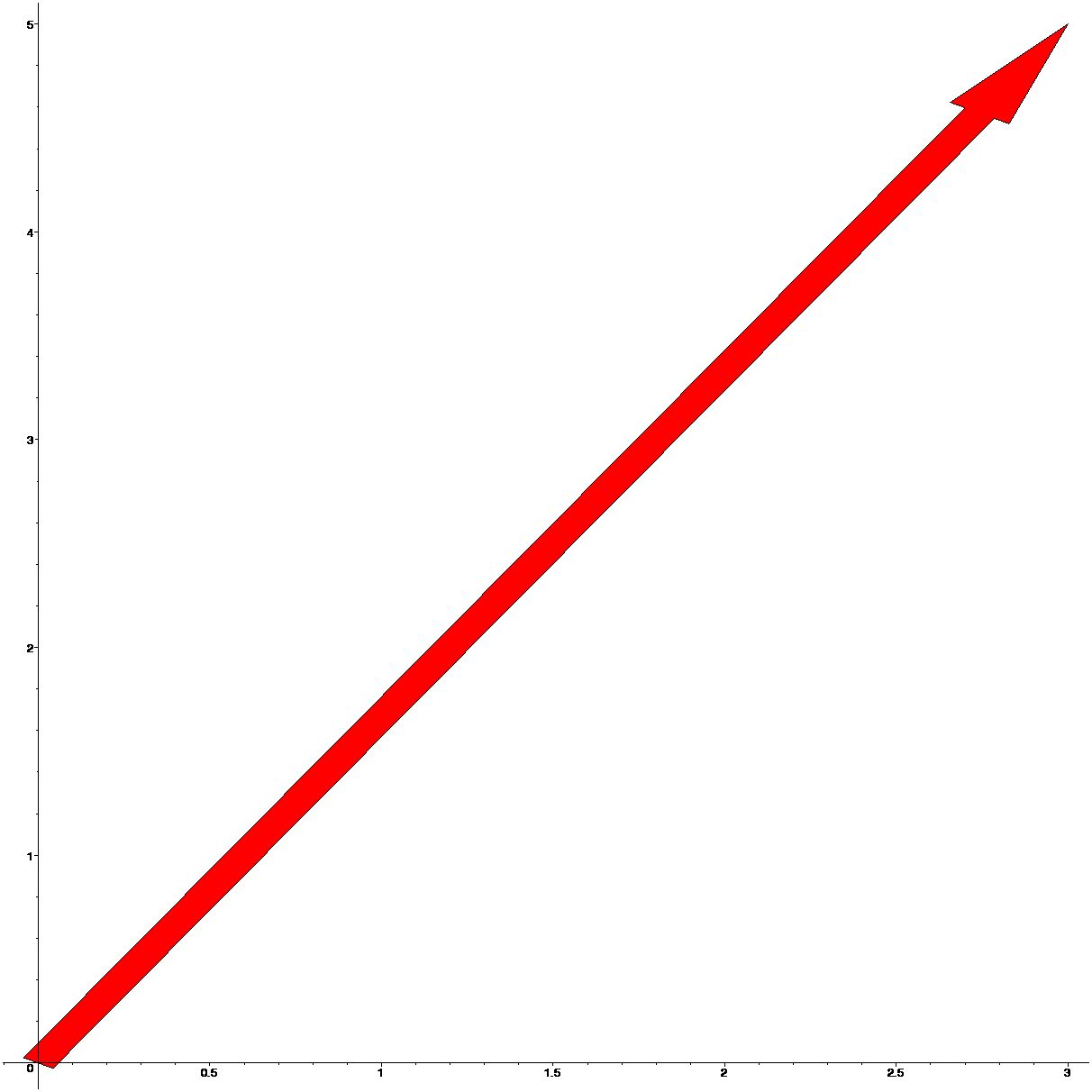
For example, in 3-dimensional plane plot the vector \(\vec v = (1,−2,4)\)
[> v:=vector([1,-2,4]);
[> V1:=arrow(v):
[> display(V1,axes=normal,labels=[x,y,z]); 
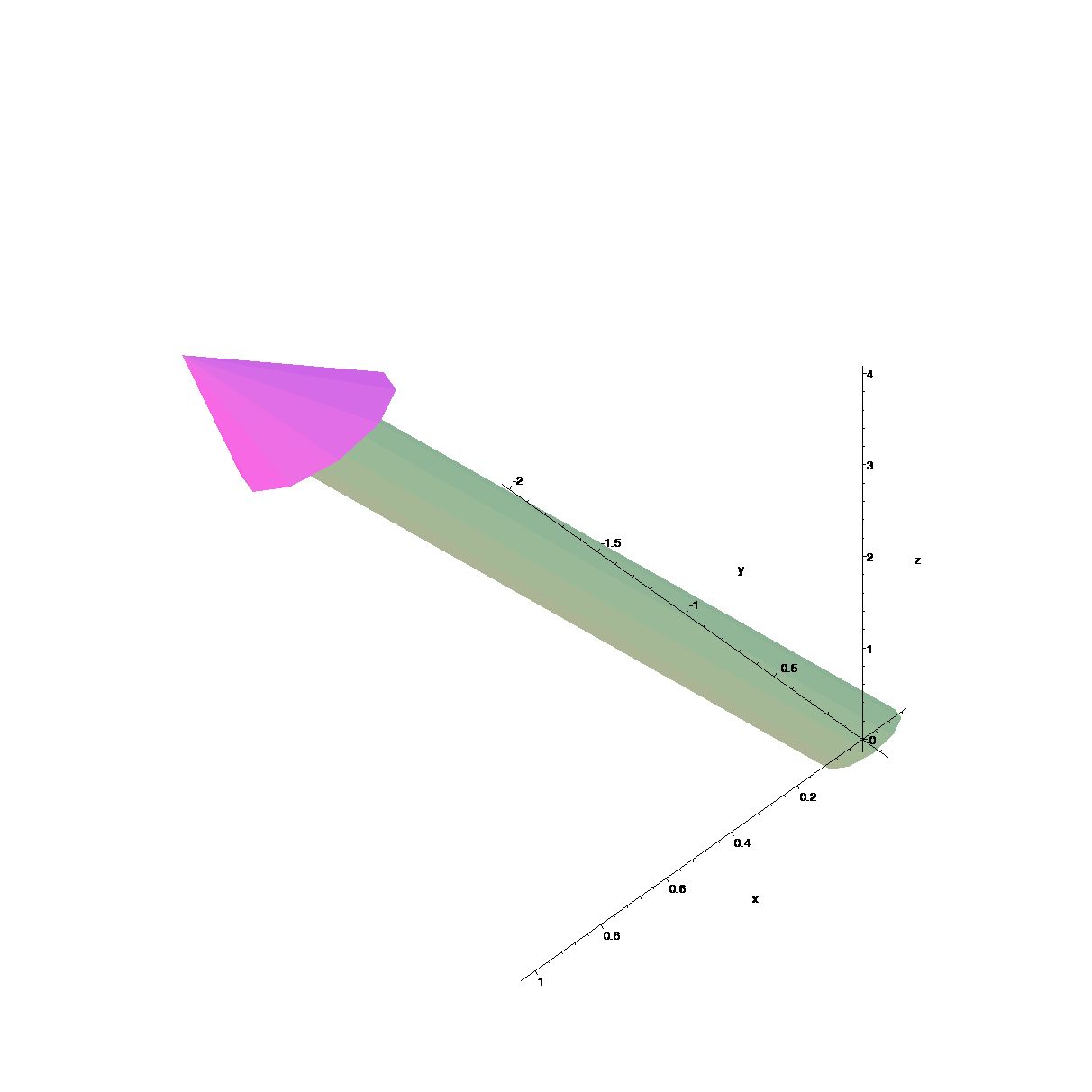
The angle of vision can be moved by clicking on the graph and moving your mouse (with the button still pressed down).
5.3.1 Sum of two vectors
The sum of two vectors \(v_1\) and \(v_2\), written \(v_1+v_2\) is the vector geometrically determined as follows.
[> restart;with(plots):
[> v1:=arrow([3,5],width=0.1,color=blue):
[> v2:=arrow([-1,2.5],width=0.1,color=red):
[> sumvectors:=arrow([3,5]+[-1,2.5],width=0.2,color=green):
[> display({v1,v2,sumvectors}); 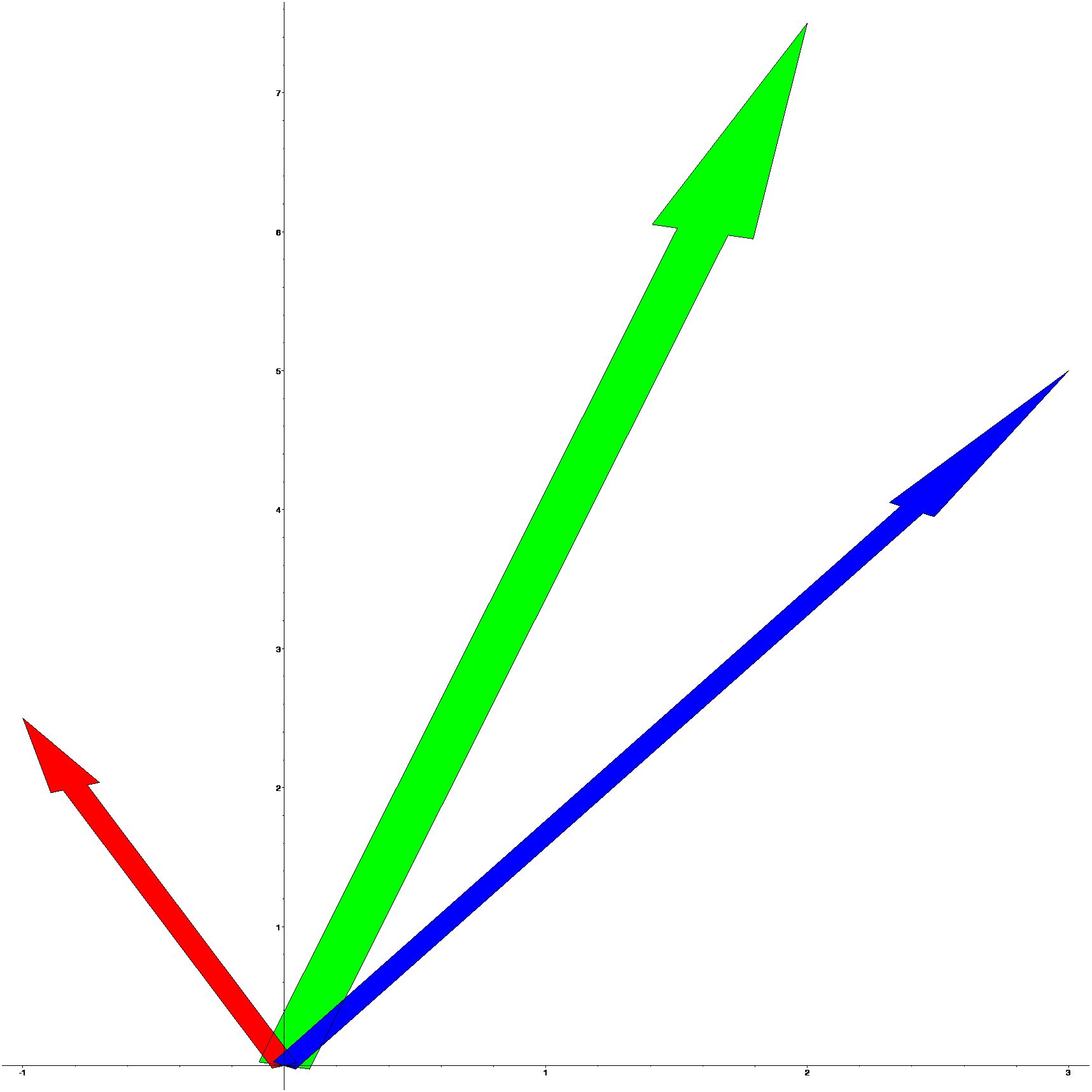
5.3.2 Difference of two vectors
If \(v_1\) and \(v_2\) are any two vectors, we define the difference of the vectors to be the vector \(v_1-v_2\) and we can construct it by plotting the sum of the vector \(v_1\) and the vector \(-v_2\).
[> restart;with(plots):
[> v1:=arrow([3,5],width=0.1,color=blue):
[> v2:=arrow([1,-2.5],width=0.1,color=red):
[> sumvectors:=arrow([3,5]+[1,-2.5],width=0.2,color=green):
[> display({v1,v2,sumvectors});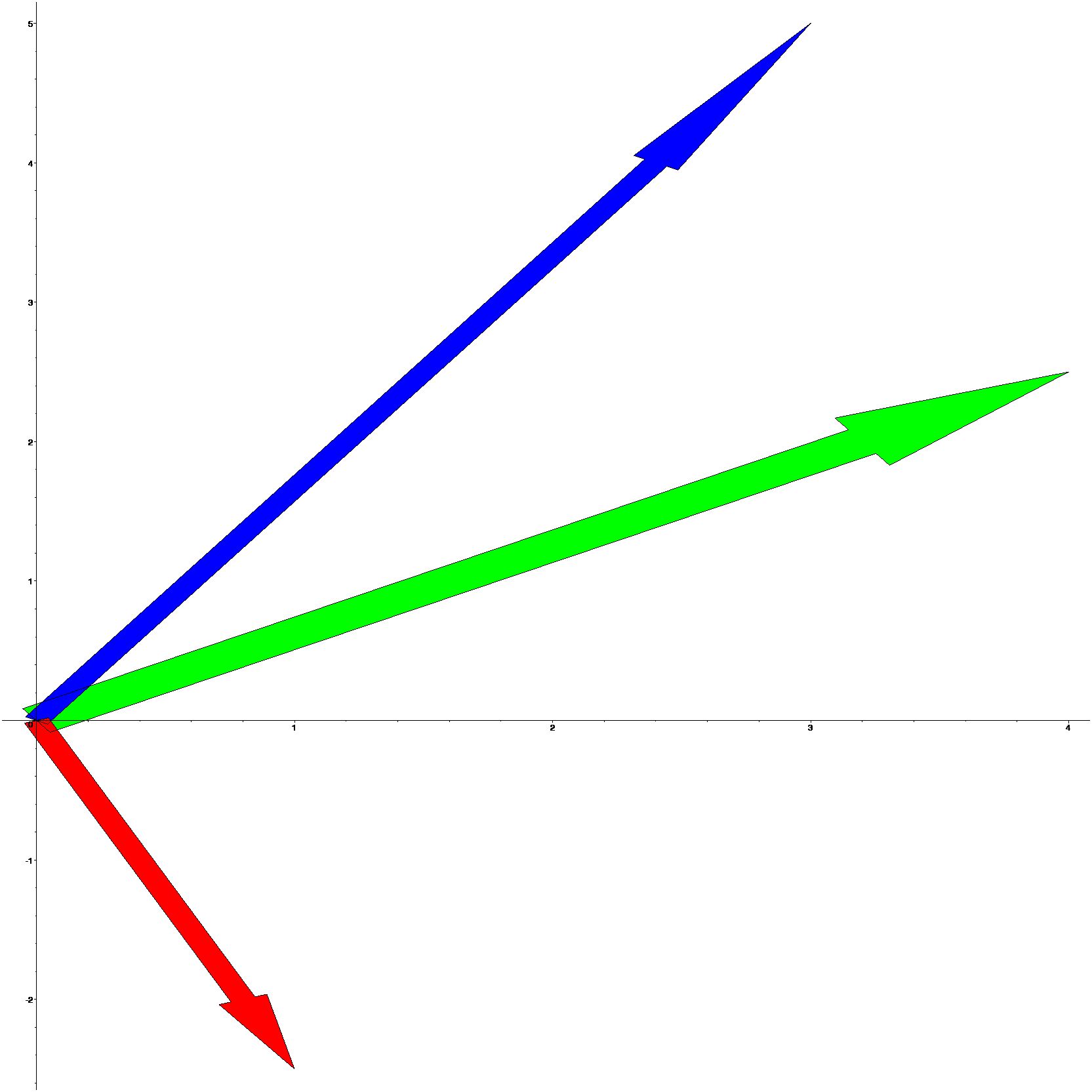
5.3.3 Multiplying a vector by a scalar
Multiplying a vector by a scalar If \(v\) is a nonzero vector and\(c\) is a nonzero scalar, we define the product of \(c\) and \(v\), denoted \(v\), to be the vector whose length is \(|c|\) times the length of \(v\) and whose direction is the same as that of \(v\) if \(c > 0\) and opposite to that of \(v\) if \(c < 0\).
[> restart;with(plots):
[> v:=arrow([3,5],width=0.5,color=blue):
[> v_times_5:=arrow([3*5,5*5],width=0.6,color=green):
[> display(v,v_times_5); 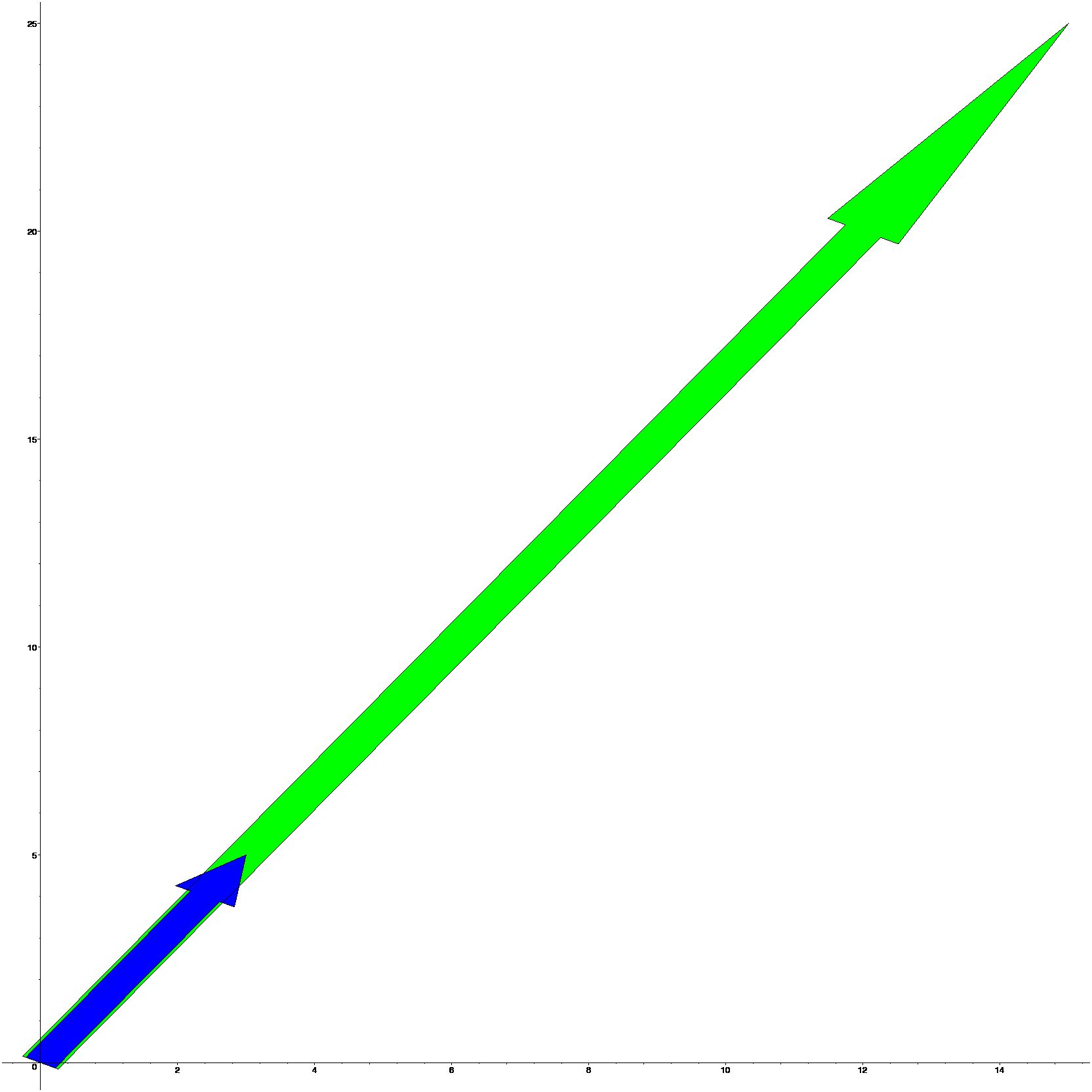
5.4 Exercises
Show that the vector \(9\mathbf{i} + \mathbf{j} - 6\mathbf{k}\) is perpendicular to the vector \(4\mathbf{i} - 6\mathbf{j} + 5\mathbf{k}\).
Find the angle between the vectors \(\mathbf{i} - 2\mathbf{j} - 2\mathbf{k}\) and \(2\mathbf{i} + \mathbf{j} - 2\mathbf{k}\).
Find \(\mathbf{a} \times \mathbf{b}\) and \(\mathbf{b} \times \mathbf{a}\) where \(\mathbf{a} = 3\mathbf{i} + \mathbf{j} + 2\mathbf{k}\) and \(\mathbf{b} = 2\mathbf{i} - 2\mathbf{j} + 4\mathbf{k}\).
Find the area of the triangle whose vertices are \(2\mathbf{i} + 3\mathbf{j} - \mathbf{k}\), \(\mathbf{i} - \mathbf{j} + 2\mathbf{k}\), and \(2\mathbf{i} + 2\mathbf{j} + \mathbf{k}\).
Find the area of the triangle whose vertices are \(\mathbf{i} + \mathbf{j} + \mathbf{k}\), \(\mathbf{i} + 2\mathbf{j} + 3\mathbf{k}\), and \(2\mathbf{i} + 3\mathbf{j} + \mathbf{k}\).
If \(\mathbf{a} = 2\mathbf{i} - 3\mathbf{j} + \mathbf{k}\), \(\mathbf{b} = \mathbf{i} - \mathbf{j} + 2\mathbf{k}\), \(\mathbf{c} = 2\mathbf{i} + \mathbf{j} + \mathbf{k}\), then find:
- \((\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c}\)
- \((\mathbf{b} \times \mathbf{c}) \cdot \mathbf{a}\)
- \((\mathbf{a} \times \mathbf{b}) \times \mathbf{c}\)
- \((\mathbf{b} \times \mathbf{c}) \times \mathbf{a}\)
For any vectors \(\mathbf{a}, \mathbf{b}, \mathbf{c}\) and any scalar \(k\), prove that:
- \(\mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c}\)
- \(k(\mathbf{a} \cdot \mathbf{b}) = (k\mathbf{a}) \cdot \mathbf{b} = \mathbf{a} \cdot (k\mathbf{b})\)
- \(\mathbf{a} \cdot \mathbf{a} = |\mathbf{a}|^2\)
- \(\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}\)
- \(k(\mathbf{a} \times \mathbf{b}) = (k\mathbf{a}) \times \mathbf{b} = \mathbf{a} \times (k\mathbf{b})\)