Lesson 10 Matrices
There are several ways to define a matrix in Maple. Use the help command to find the general definition of a matrix. To work with Matrices first load the package linalg Which include most linear algebra related commands.
10.1 Defining matrices
There are several ways to define Matrix. Let’s look at them through examples.
You can use maple help.
> ? matrix> restart;
> with(linalg):
> M1 :=matrix (3, 3, [1,-2,-3,2,-2,2,3,-3,3]);
> M2:= matrix(3,4,[1,1/2,-1/3,1/4,2,1/2,-3/4,5/4,3,3/5,3/7,3/8]);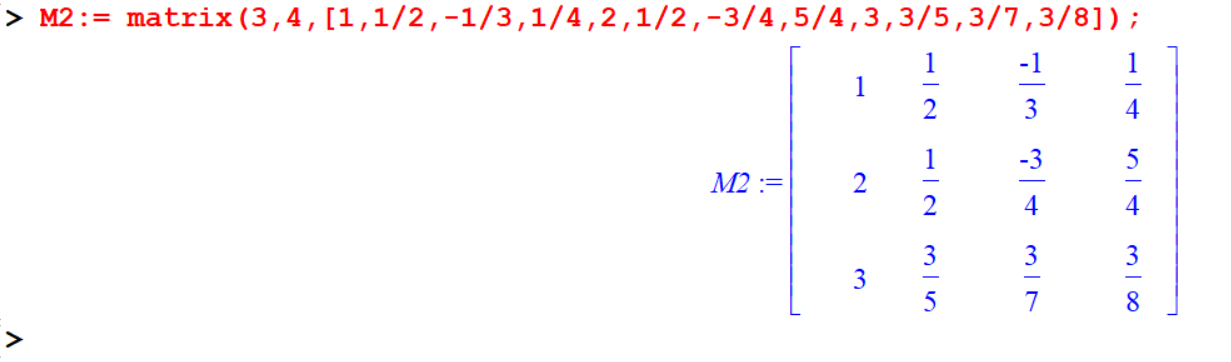
[> A:= matrix(3,3,[[1,-3,-2],[2,-3,5],[-4,2,6]]);
[> B:=matrix([[1,-3,-2],[2,-3,5],[-4,2,6]]);
[> Matrix (2,2,fill=a);
[> Matrix (2,2,symbol=a);
[> f:=i->x*i-1;
[> M:=Matrix(2,f);
[> g:=(i,j)->x*(i+j—l);
[> M1:=Matrix(3,g); To define a diagonal matrix.
To define a diagonal matrix.
[> C:=diag(1,2,3);
[> diag(1,1,1);
To define lower triangular matrix.
[> M_1:=Matrix(3,[[x],[y,y],[z,z,z]],shape=triangular[lower]);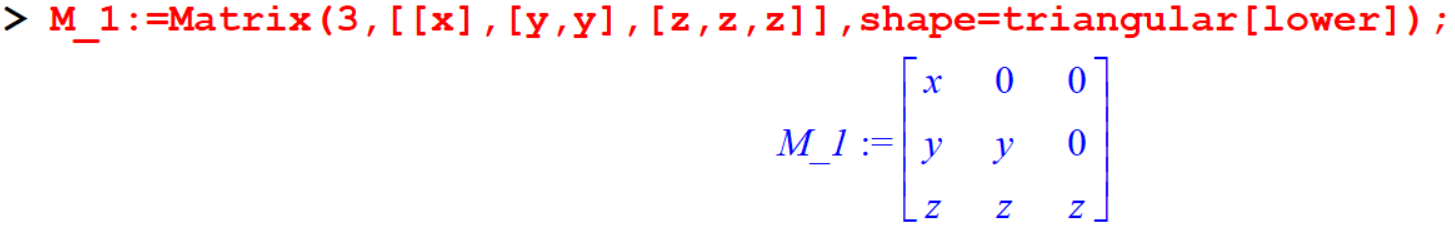
[> M_2:=Matrix(3,[[1,2,3],[4,5,6],[7,8,9]],shape=triangular[upper]);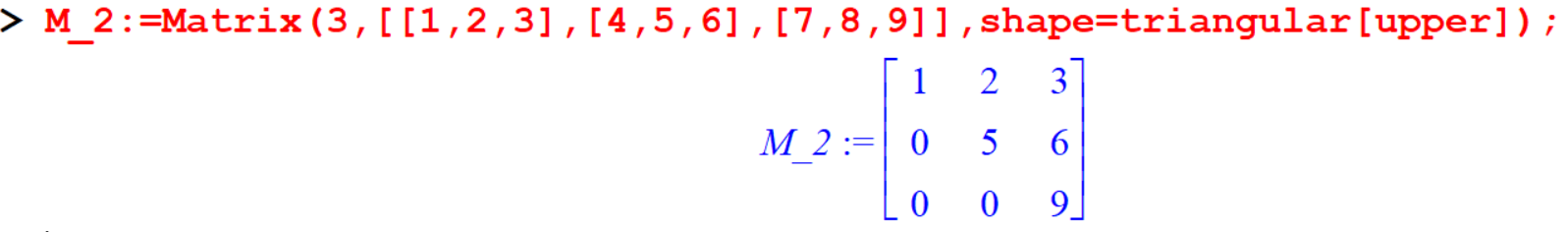
To define zero matrix
[> M_3:=Matrix(4,4,shape=zero);
To define identity matrix
[> M_3:=Matrix(3,3,shape=identity);
To find an entry of a matrix, follow the name of the matrix by indices inside a square bracket.
[> A:= matrix(3,3,[[1,-3,-2],[2,-3,5],[-4,2,6]]);
[> A[3,2];
[> B:=matrix([[1,-3,-2],[2,-3,5],[-4,2,6]]);
[> B[1,2]; ## Matrix Operation
## Matrix Operation
10.2 Row Opreations
In your linear algebra class you will learn elementary row operations on matrices here we will use Maple to do the same thing. Let’s define a new matrix \(A\).
- addrow(A,r1,r2,m)
Returns a copy of a matrix \(A\) in which row r2 replaced with by row(A,r2)+m*row(A,r1)
[> A:=matrix([[1,4,3,10],[2,1,-1,-1],[3,-1,4,11
[> addrow(A,1,2,-2);
[> addrow(%,1,3,-3);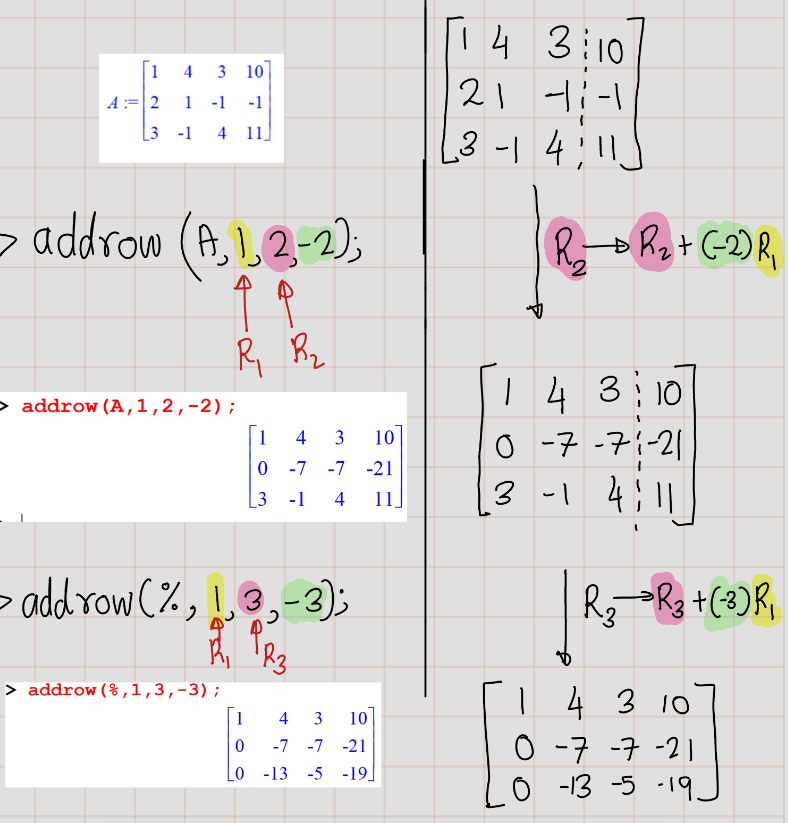
- mulrow(A,row,expr)
Returns a matrix \(A\) in which has the same entries as \(A\) with the \(r^{th}\) row mutiplied by \(expr\)
[> mulrow(A,2,-1/7);
[> mulrow(%,3,-1/3);
- swaprow(A,r1,r2)
This command interchange row r1 and r2 of \(A\)
[> swaprow(A,2,3);
Similarly, you can learn addcol, mulcol,swapcol commands by your self.
10.3 Determinanat of Matrix
To find the determinate of a matrix, maple has a special command det.
[> M1 :=matrix (3, 3, [1,-2,-3,2,-2,2,3,-3,3]);
[> det(M1);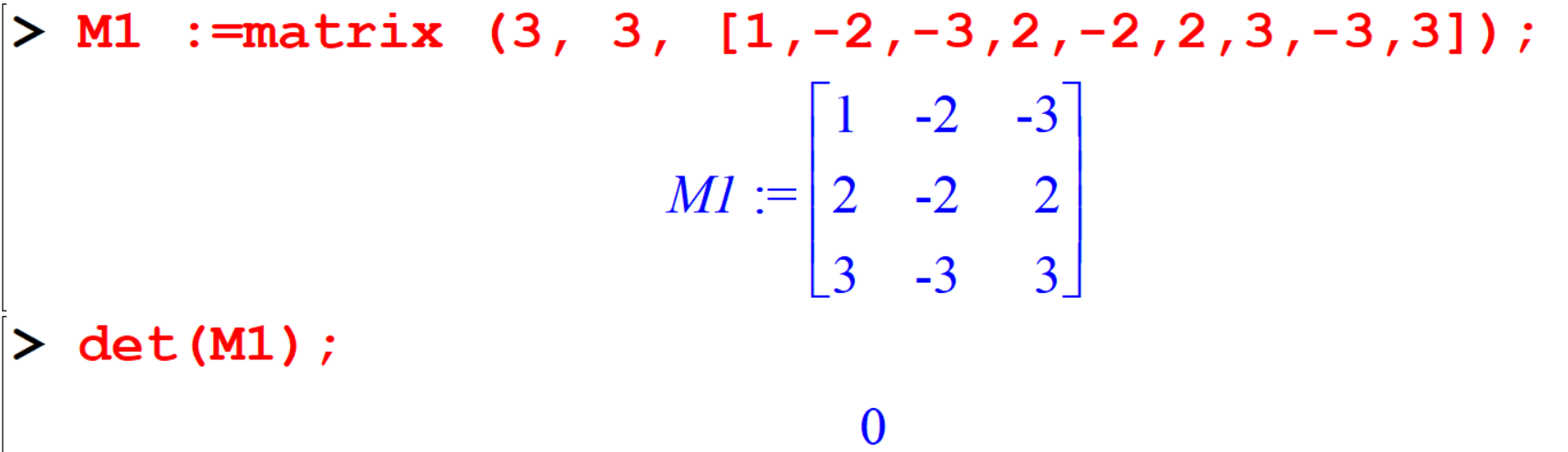
[> B:=matrix([[1,-3,-2],[2,-3,5],[-4,2,6]]);
[> det(B);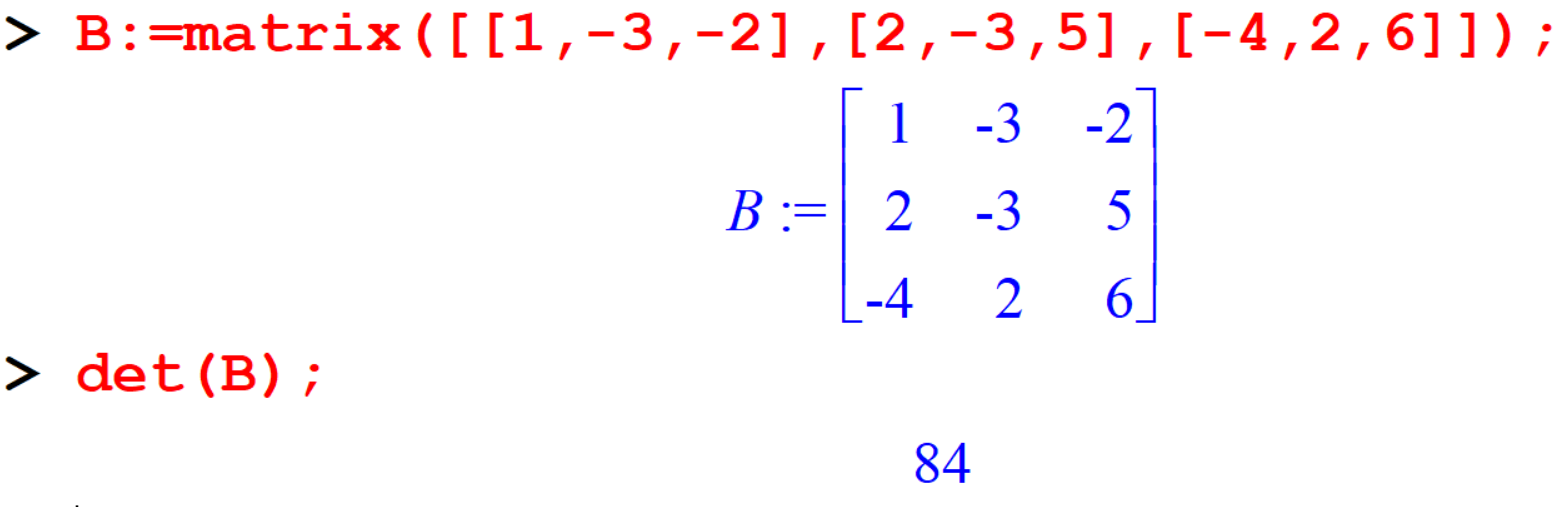
10.4 Exercise
Exercise 10.1 Performs the indicated computations.
A. \(\begin{bmatrix} 1 & 0 & 3 \\ 2 & -1 & 6 \end{bmatrix}+ \begin{bmatrix} 2 & 0 & 4 \\ -2 & 5 & 8 \end{bmatrix}\)
B. \(5 \begin{bmatrix} 2 & 1 & 3 \\ -1 & 2 & 4 \\ -6 &1 & 5 \end{bmatrix} -3 \begin{bmatrix} -2 & 1 & 4 \\ 5 & 0 & 7\\ 2 & -1 &3 \end{bmatrix}\)
C. \(\begin{bmatrix} 2 & 3 \\ -1 & 4 \end{bmatrix} \begin{bmatrix} 5 & -1 \\ 2 & 7 \end{bmatrix}\)
D. \(\begin{bmatrix} 2 & 3 & 1 & 5 \\ 0 & 6 & 2 & 4 \end{bmatrix} \begin{bmatrix} 5 & 7 & 1 \\ 2 & 0 & 3 \\ 1 & 0 & 0 \\ 0 & 5 & 6 \end{bmatrix}\)
E. \(\begin{bmatrix} 2 & 4 & 3 \\ 1 & 3 & 5 \end{bmatrix} \begin{bmatrix} 0 & 7 & 4 \\ 2 & 3 & 0 \end{bmatrix}\)
F. \(3 \begin{bmatrix} -2 & 1 \\ 0 & 4 \\ 2 & 3 \end{bmatrix}\)
G. \(\begin{bmatrix} 1 & 0 & 3 & -1 & 5 \\ 2 & 1 & 6 & 2 & 5 \end{bmatrix} \begin{bmatrix} 7 & 1 \\ 2 & 3 \\ -1 & 0 \\ 5 & 6 \\ 2 & 3 \end{bmatrix}\)
H. \(\begin{bmatrix} 1 & -1 & 2 \\ 3 & 5 & 6 \\ 2 & 4 & -1 \end{bmatrix} \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix}\)
Exercise 10.2 Determine the given matrices are invertible. If they are, compute the inverse.
A. \(\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix}\)
B. \(\begin{bmatrix} 1 & 1 & 1 \\ 0 & 2 & 3 \\ 5 & 5 & 1 \end{bmatrix}\)
C. \(\begin{bmatrix} a & a \\ b & b \end{bmatrix}\)
D. \(\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix}\)
E. \(\begin{bmatrix} 5 & 7 & 0 \\ 2 & 1 & 3 \\ 1 & 0 & 0 \\ 0 & 4 & 3 \end{bmatrix}\)
F. \(\begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & -1 & 2 \\ 1 & -1 & 2 & 1 \\ 1 & 3 & 3 & 2 \end{bmatrix}\)
G. \(\begin{bmatrix} 1 & -3 & 0 & 2 \\ 3 & -12 & -2 & -6 \\ -2 & 10 & 2 & 5 \\ -1 & 6 & 1 & 3 \end{bmatrix}\)
Exercise 10.3 Compute the \(3\times 3\) matrix whåse entries are given by the function \(y^{ij}\), Where \(i = j = 1, 2, 3\).
Exercise 10.4 Compute the matrix,\(\begin{bmatrix} x & x^2 \\x^2 & x^3 \end{bmatrix}\) by defining a suitable function as in the exercise 10.3
Exercise 10.5 Which of the following matrices are skew-symmetric? (A square matrix a symmetric if \(A^T = -A\), where \(A^T\) is the transpose of \(A\).)
A.\(\begin{bmatrix} 1 & -6 \\ 6 & 0 \end{bmatrix}\)
B.\(\begin{bmatrix} 0 & -6 \\ 6 & 0 \end{bmatrix}\)
C.\(\begin{bmatrix} 2 & -2 & 2 \\ 2 & 2 & -2 \\ 2 & 2 & 2 \end{bmatrix}\)
D.\(\begin{bmatrix} 0 & 1 & -1 \\ -1 & 0 & 2 \\ 1 & -2 & 0\end{bmatrix}\)
Exercise 10.6 Convert the following matrix in to an upper triangular matrix. \[\begin{bmatrix} 2 & 3 & -1 \\ -3 & -2 & 1 \\ 0& 1 & 1\end{bmatrix}\]
Exercise 10.7 Convert the following matrices into a identity matrix.
A.\(\begin{bmatrix} 2 & 7 & 3 \\ 1 & 3 & 2 \\ 3 & 7 & 9\end{bmatrix}\)
B.\(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\)