Lesson 12 Intergration
The int command is used to compute both definite and indefinite integrals of Maple expressions as shown by the following examples.
12.1 Indefinite Integration
[> int(x^2,x);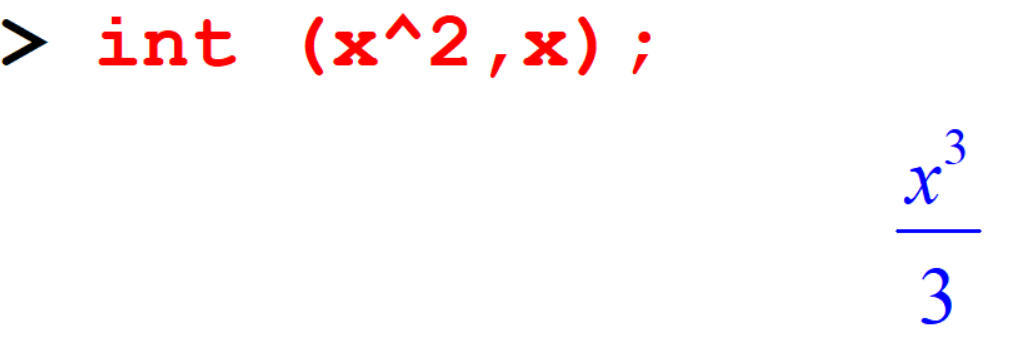
[> int(sin(2*t),t);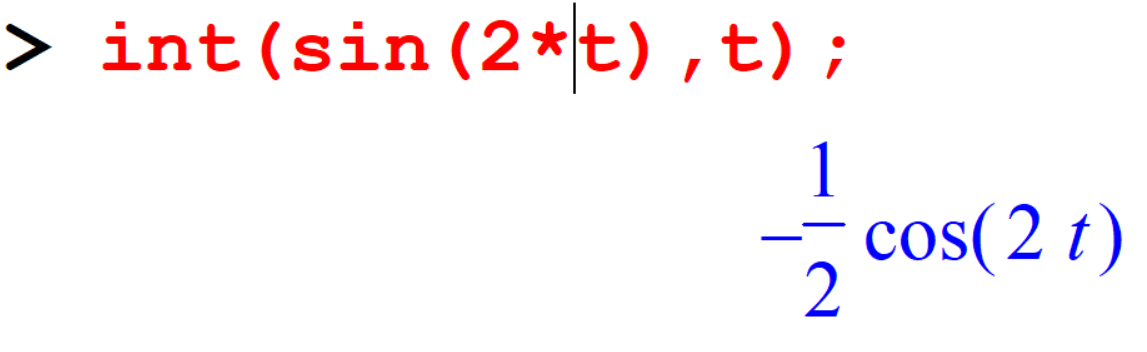
[> f:=x->(3*x-6)/(x^2-4);
[> int(f(x),x);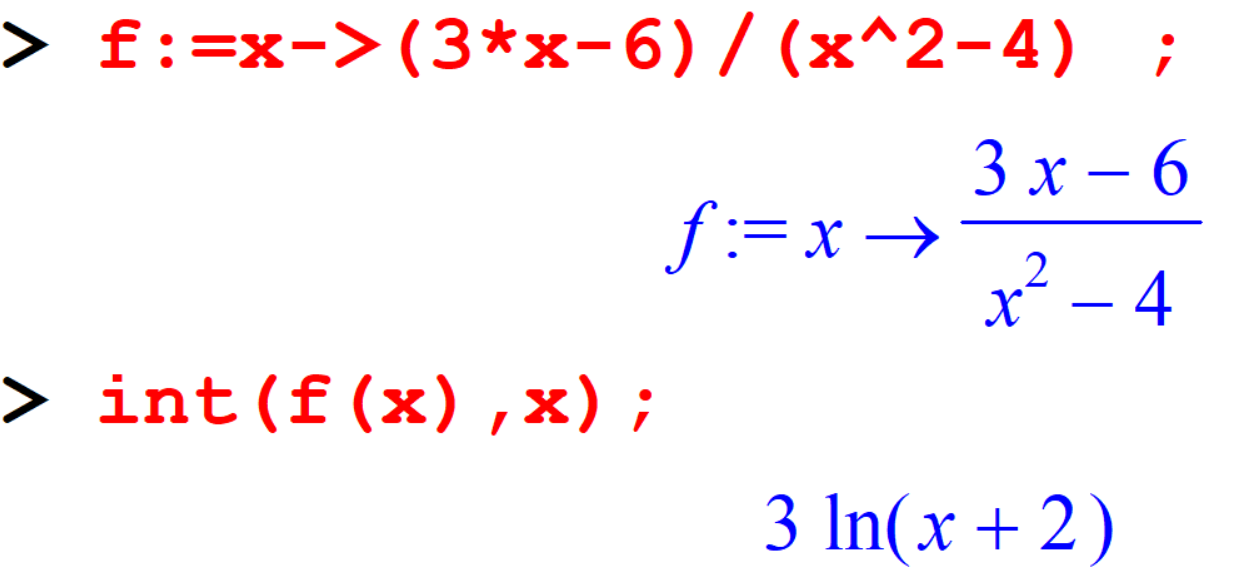
[> Int(sin(x),x);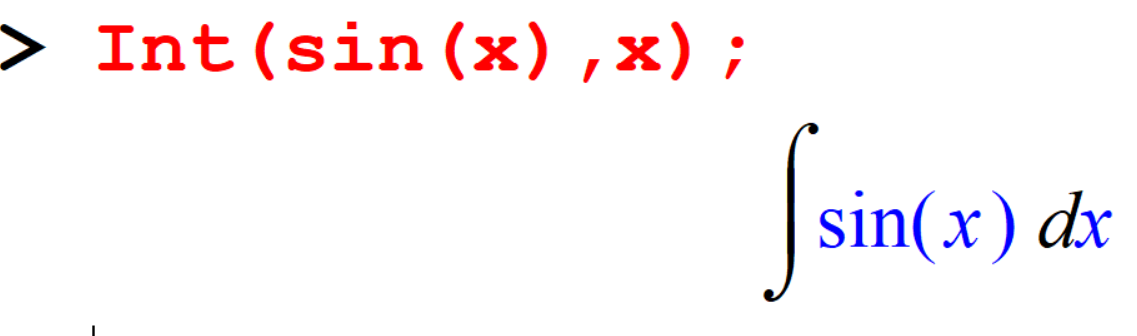
[> Int(3*x^2+2)^(5/3),x);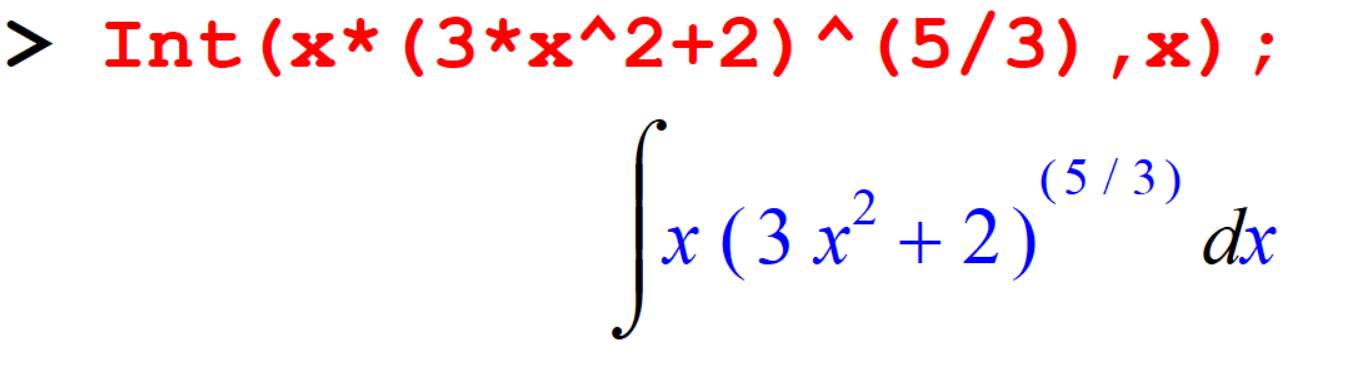
[> Int(x*(3*x^2+2)^(5/3),x)=int(x*(3*x^2+2)^(5/3),x);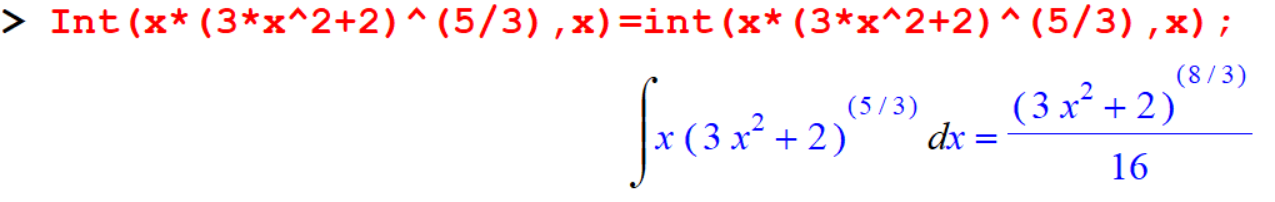
Notice that Maple doesn’t include a constant of integration for indefinite integrals. Where there are constants, Parameters other variable around, Maple assume that you mean to take the integral as the variable you specify changes, and that all other letters in the expression represent constants.
12.2 Definite Integration
[> Int(g(x),x=a..b);
[> Int(x^2*exp(x),x=0..2)=int(x^2*exp(x),x=0..2);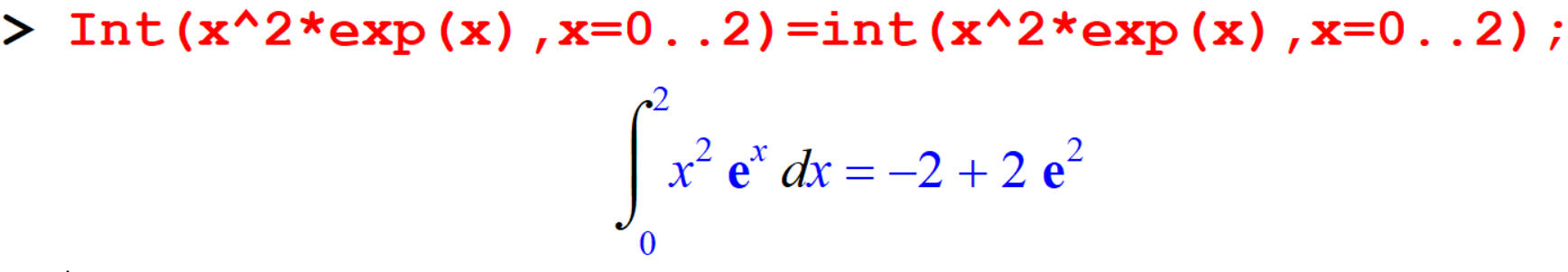
[> f := x -> x*sin(x);
[> int(f(x),x=0..Pi);
Some functions can not be integrated analytically, but the definite integrals of such functions still have meaning and MAPLE can determine them.
[> int(exp(-x^2)*ln(x),x);
[> int(exp(-x^2)*ln(x),x=0..infinity);
[> evalf(%);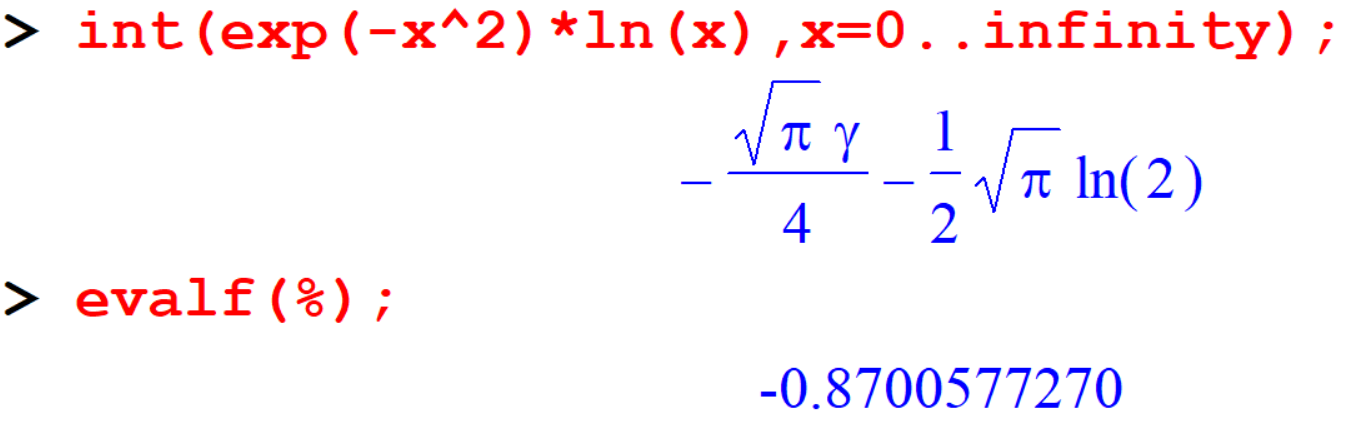
12.3 Integration by Parts
The intparts command is used to integrate by parts, and the command exist in student package.
The intparts command has two arguments: the first is the expression to be anti-differentiated, and the second is the choice for, the piece which is to be differentiated.
\[ \int u D(v) dx = uv - \int v D(u) dx \]
Example 12.1 Method of integration by parts to compute \(\int x \cos(x)\)
[> restart;
[> with(student):
[> p1:= Int(x*cos(x),x);
[> p2:= intparts(p1,x);
[> p3:= value(p2);
[> p1 = p3 + C;
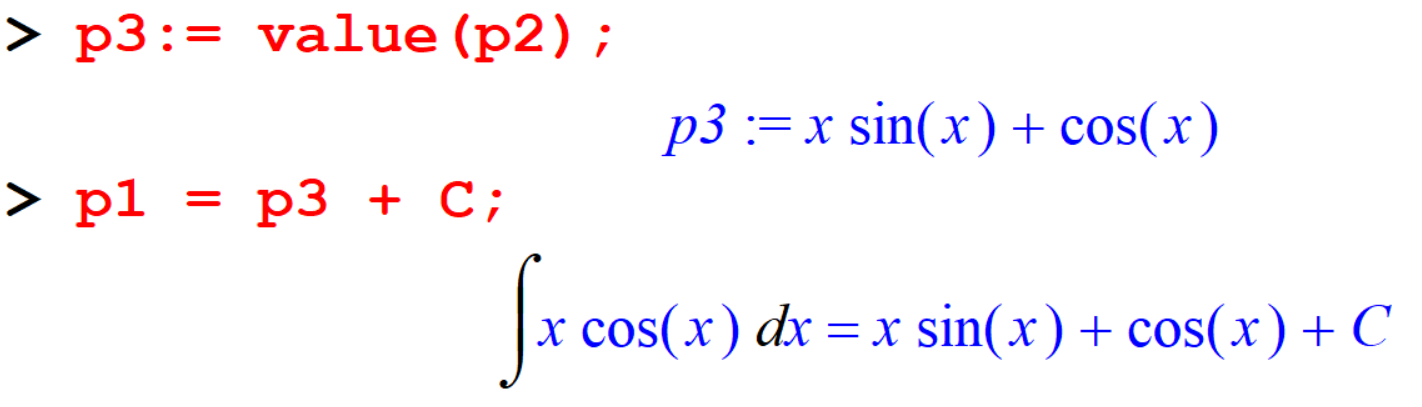
[> restart;
[> with(student):
[> Int(sqrt(x)*ln(x),x)=intparts(Int(sqrt(x)*ln(x),x),ln(x));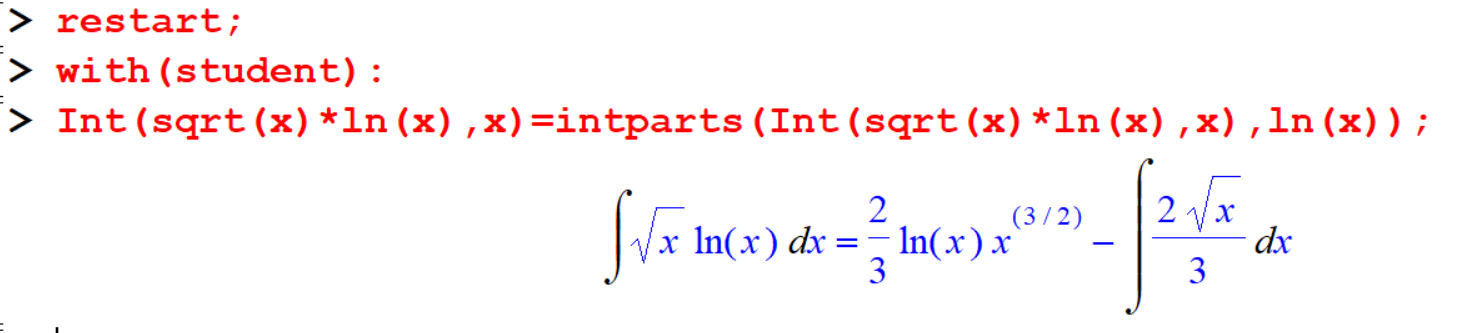
[> Int(sqrt(x)*ln(x),x)=value(intparts(Int(sqrt(x)*ln(x),x),ln(x)));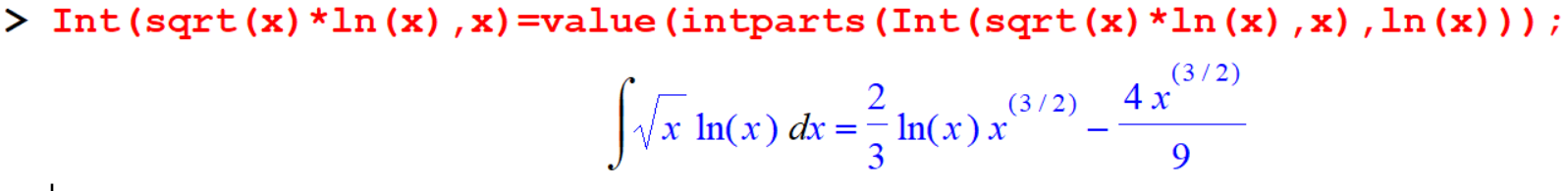
12.4 Substitutions
These are done using the changevar command. Look at the following example.
Example 12.2 Evaluate \(\int 4 \cos(\sin(x)) dx\) using the substitution, \(u=\cos(x)\) .
[> Int(cos(x)^4*sin(x),x)=changevar(u=cos(x),Int(cos(x)^4*sin(x),x),u);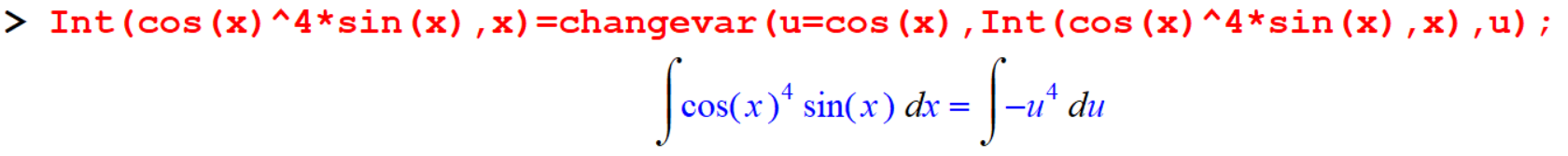
[> v1:=value(changevar(u=cos(x),Int(cos(x)^4*sin(x),x),u));
To back-substitute, we use the subs command,
[> subs(u=cos(x),v1);
12.5 Multiple Integration
12.5.1 Double integration (Area calculation)
[> Int(Int(x^2+2*x,x),x);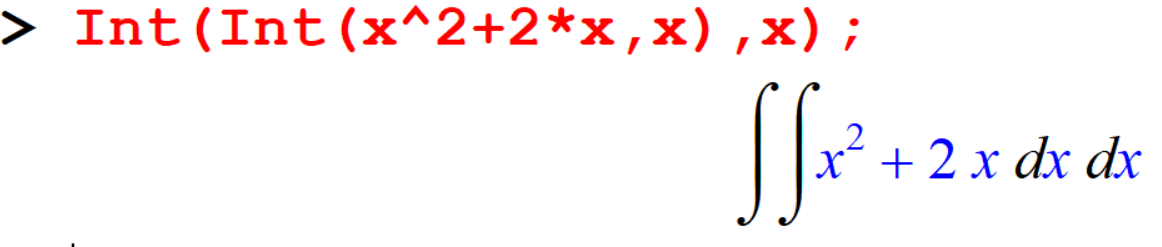
[> int(int(x^2+2*x,x),x);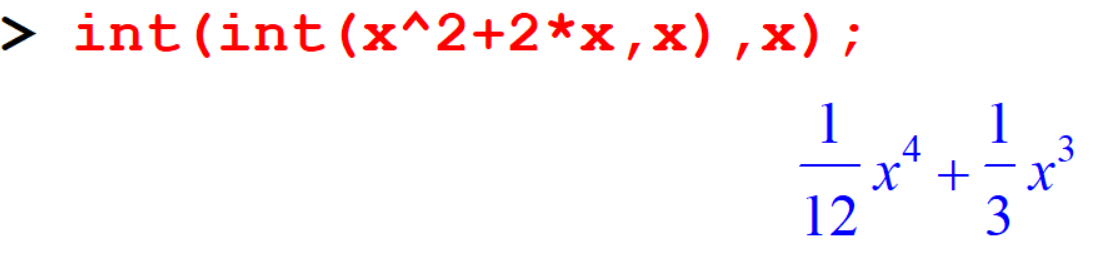
[> Int(Int(x+y^2,y=0..x),x=1..2);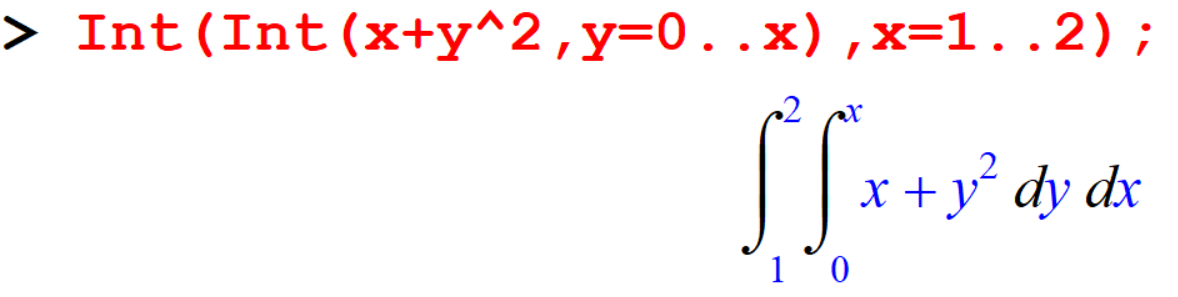
[> a:=Int(x+y^2,y=0..x);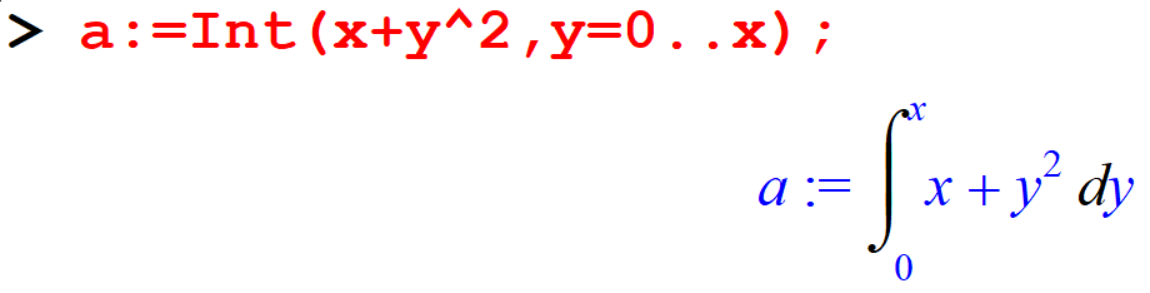
[> b:=Int(a,x=1..2);
[> Int(Int(x+y^2,y=0..x),x=1..2)=int(int(x+y^2,y=0..x),x=1..2);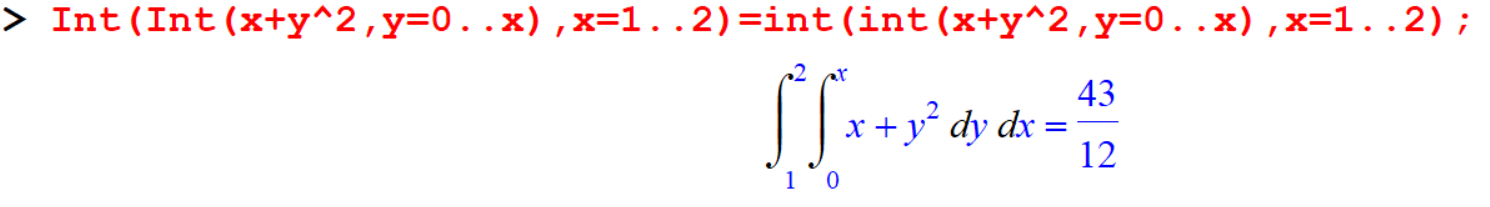
[> A:=Doubleint(x+y^2,y=0..x,x=1..2);
[> value(A);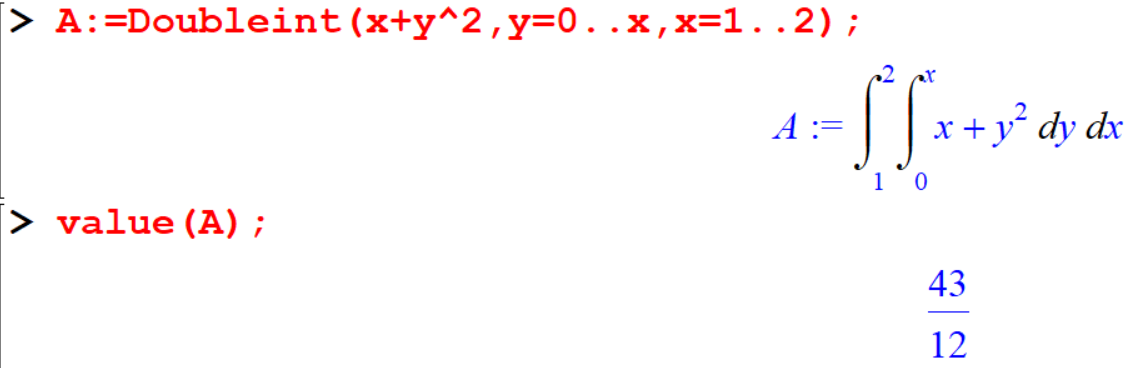
12.5.2 Triple integration (Volume Calculation)
[> Int(Int(Int(x^3*exp(y)*sin(z),x=0..2),z=-Pi..2*Pi),y=0..1)=int(int(int(x^3*exp(y)*sin(z),x=0..2),z=-Pi..2*Pi),y=0..1);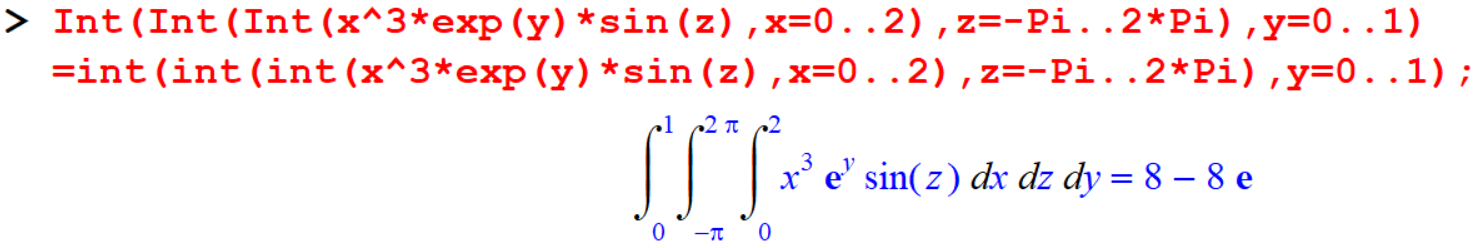
[> V:=Tripleint(x^3*exp(y)*sin(z),x=0..2,z=-Pi..2*Pi,y=0..1);
[> value(V);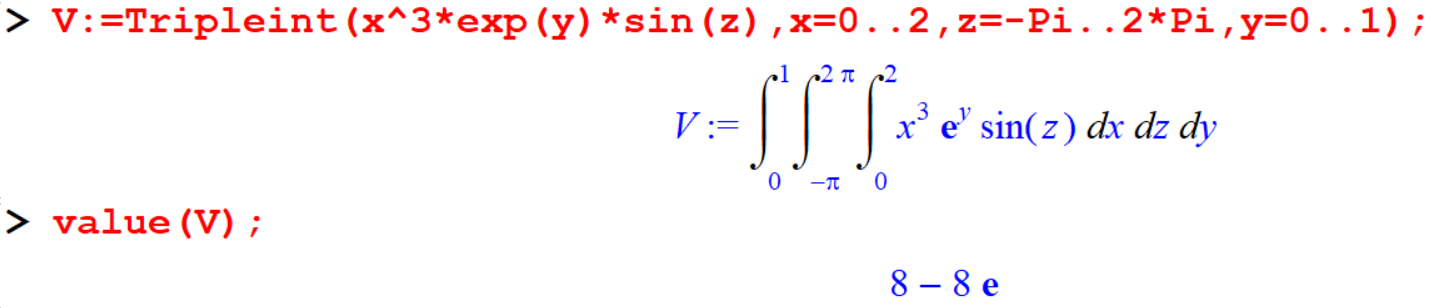
Note: Since there is often more than one way to find an indefinite integral, it may happen that the answer you obtain by doing the techniques seen in class is different than the one obtained with Maple.
12.6 Exercise
Exercise 12.1 Integrate the following expressions,
- \(2x^2 + \frac{x}{2}\)
- \(x^3(3x^2 + 2)^{\frac{5}{3}}\)
- \(e^{-x^2}\)
Exercise 12.2 Find the definite integral of the following over the given intervals,
- \(\int_{2}^{10} x^3(3x^2 + 2)^{\frac{5}{3}} \, dx\)
- \(\int_{0}^{\frac{\pi}{2}} \cos(x) \sin(x^2) \, dx\)
- \(\int_{0}^{\pi} e^x \cos(x) \, dx\)
- \(\int_{0}^{\pi} e^{2\sin(x)}\cos(x) \, dx\)
Exercise 12.3 Use of the method of integration by parts to compute,
- \(\int x e^{-2x} \, dx\)
- \(\int x \ln(x) \, dx\)
Exercise 12.4 Evaluate the following expressions
- \(\int_{-3}^3 \int_{-3}^3 3x^2 + 5y^2 +4 \, dxdy\)
- \(\int_{-3}^3 \int_{-3}^3 9 \ln(x) - 5y^2 \, dxdy\)
Note: Since there is often more than one way to find an indefinite integral, it may happen that the answer you obtain by doing the techniques seen in class is different than the one obtained with Maple. Compare the answers obtained by Maple and the answer you obtained manually for the integral, \(\int \cos(3x)\,dx\)
There are two main ways to use the definite integral. - The easiest one to understand is as a means for computing areas (and volumes). - The second way the definite integral is used is as a sum. That is, we use the definite integral to ``add things up’’.
12.7 Computing the area from the integral
Example 12.3 Find the area under the curve \(x^2\sin(x)\)
[> int(x^2*sin(x),x=-Pi..Pi);[> plot(x^2*sin(x),x=-Pi..Pi);[> a1:=int(x^2*sin(x),x=-Pi..0);`[> a2:=int(x^2*sin(x),x=0..Pi);
[> abs(a1)+a2;Example 12.4 Find the area bounded by the curves \(−x^2 +4x + 6\) and \(\frac{x}{3}+2\)
[> f := x-> -x^2+4*x+6;
[> g := x-> x/3+2;
[> plot({f(x),g(x)},x=-2..6);
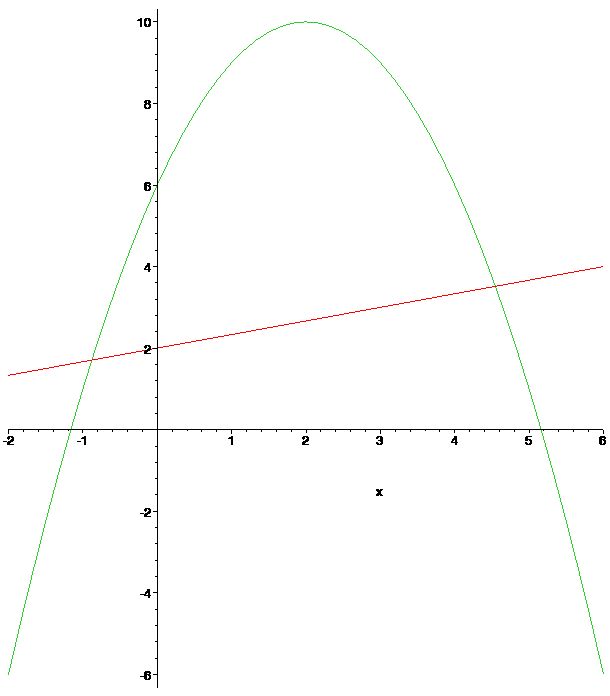
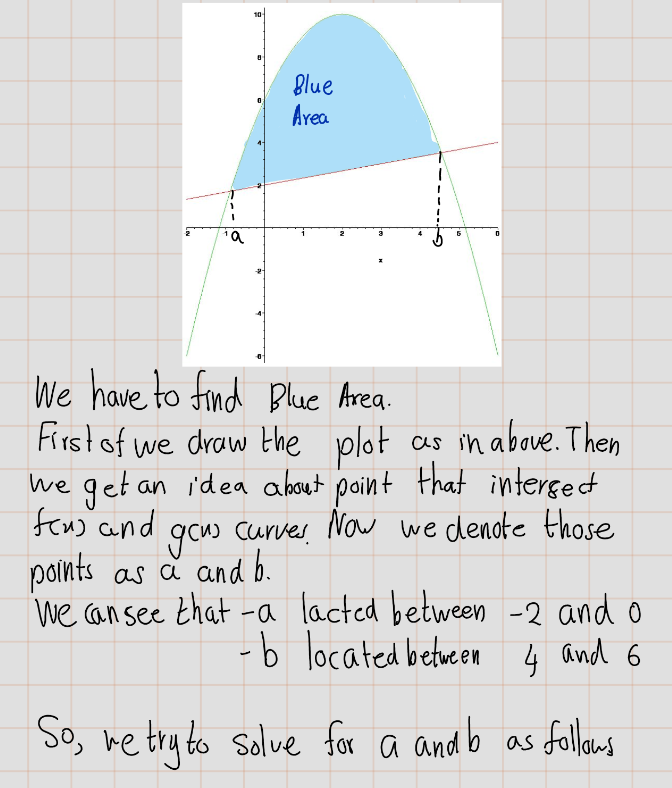First we find \(a\) and \(b\).
[> a := fsolve(f(x)=g(x),x=-2..0);
[> b := fsolve(f(x)=g(x),x=4..6);
[> Area:=int(f(x)-g(x),x=a..b);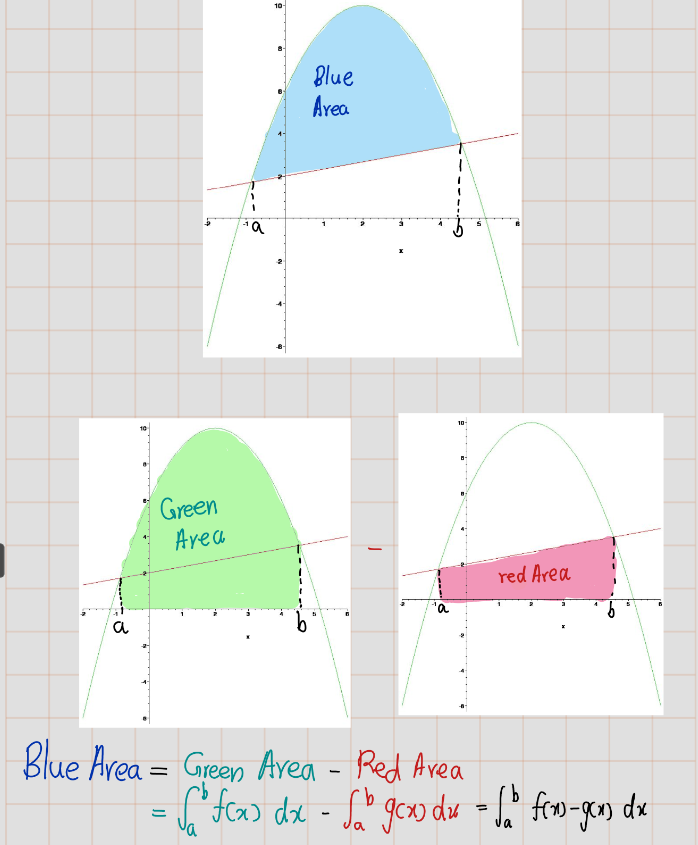
Alternative Method
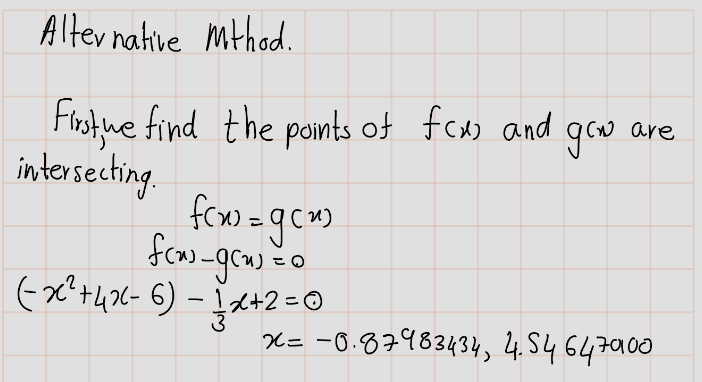
[> evalf(solve(-x^2+4*x+6-x/3-2,x));
[> Area:=int(f(x)-g(x),x=-.8798034327..0)+int(f(x)-g(x),x=0..4.546470099);Example 12.5 Find the area of the region enclosed between the two curves \(f(x)=2x+5\) and \(g(x)=x^2+2\) from \(x=0\) to \(x=6\).
[> g:=x->x^2+2;f:=x->2*x+5;
[> plot({f(x),g(x)},x=-2..7,color=[red,blue]);
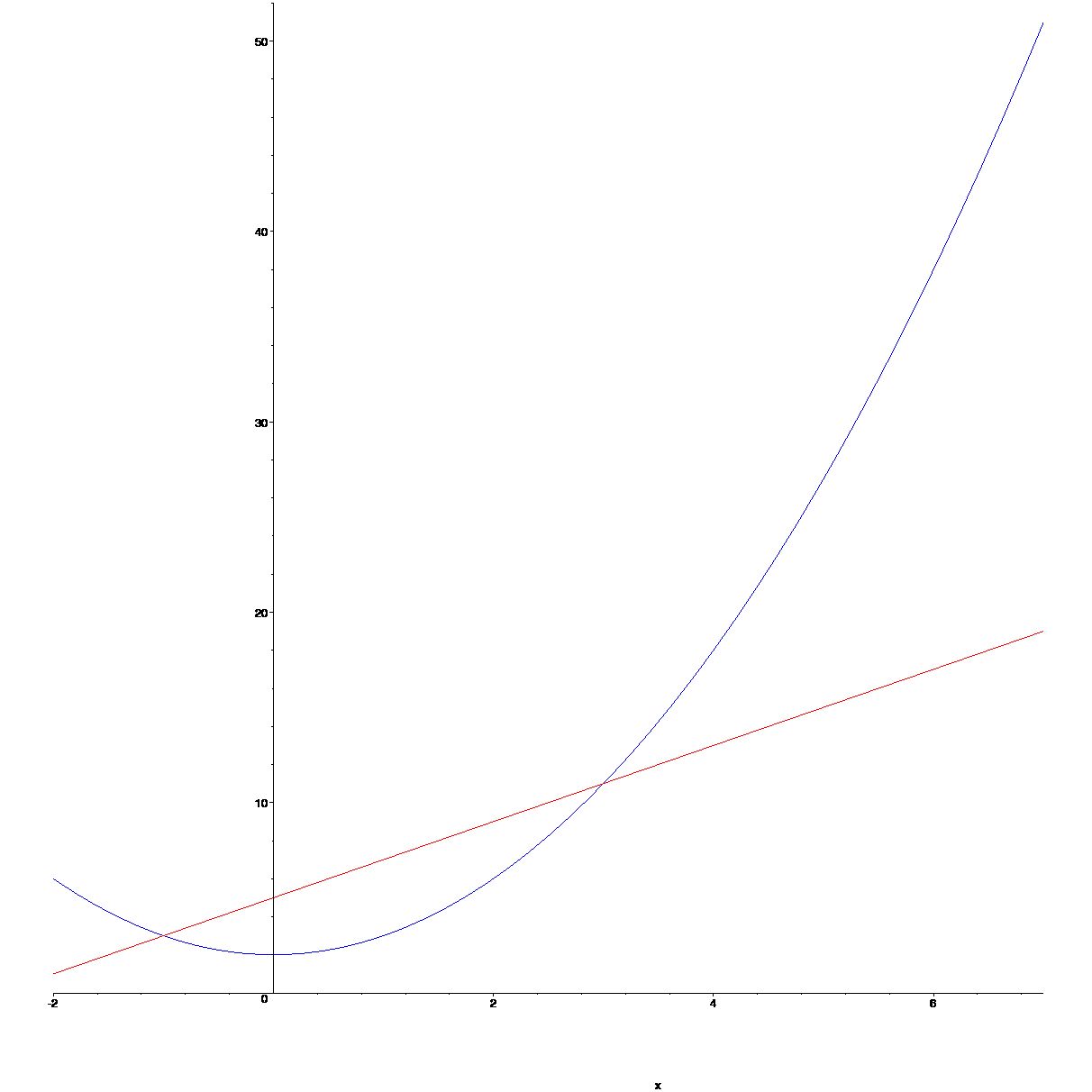
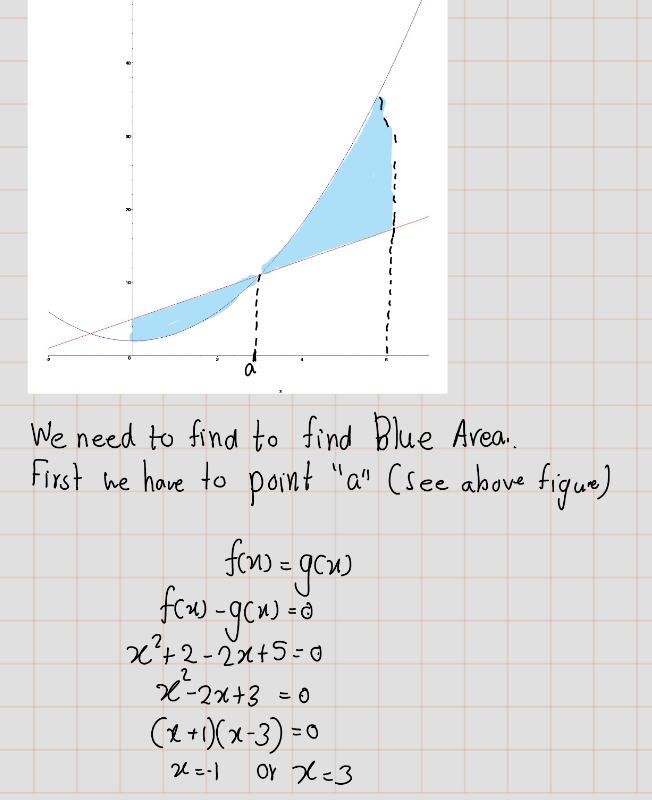
[> solve(x^2+2-2*x-5,x);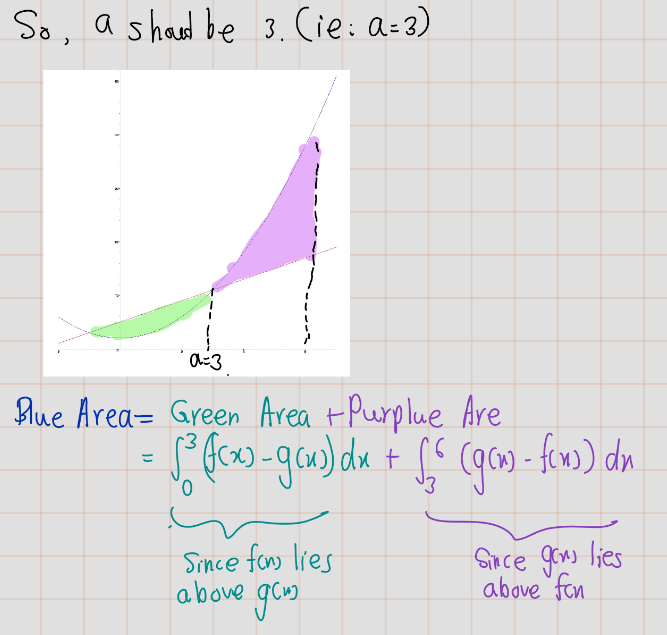
[> Area:=int(f(x)-g(x),x=0..3)+int(g(x)-f(x),x=3..6);