Lesson 6 Set Theroy

6.1 Set Definition and Cardinity

A set is an unordered collection of objects that we usually denote by capital letters. The objects in a set are called its elements, or members, which are contained by the set.

[> A:={a,b,c,d,e}; 
[> B:={1,2,3,4}; 
[> ES:={};

In the following you can see that Maple can generate sets with large number of elements.

[> P:={seq(i*2,i=1..10)};
[> Q:={seq(2*i-1,i=1..10)};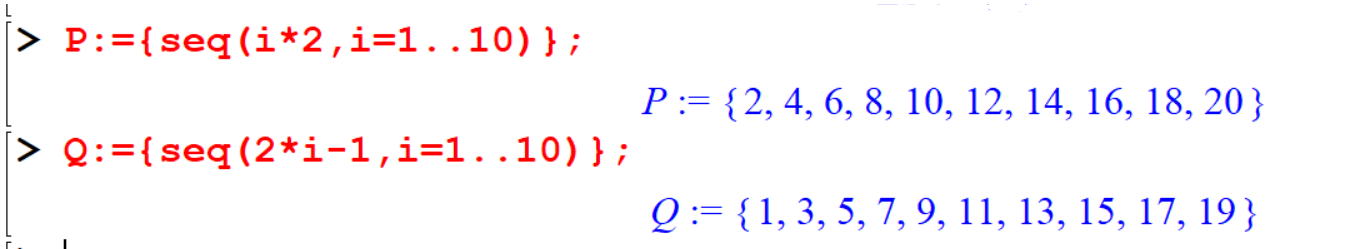

Usually nops command is used to count the number of operands in an expression and when applied to a finite set it returns the cardinality of the set.

[>nops(A)]
[> nops({red,green,blue});

6.2 Checking for the set membership

[> a in A; 
[> p in A;

You can see the above command would not give required results. To avoid those, you can use the evalb command to check whether a given object is an element of the predefined set or not. This function evaluates to Boolean, whose result is printed out as one of either of the two Boolean constants true or false.

> evalb(a in A); 
> evalb(p in A);

The elements of a set can be extracted via the selection operation. Thus if \(A\) is a set then A[i] selects the \(i\) th element. Alternatively you may use op(i,A).

6.3 Set Operations

6.3.1 Subsets

[> {a,b,c} subset A; 
[> {3,4,5} subset B;              
[> {x,y} subset {x,y,z};

Or

> `subset`({x,y},{x,y,z});

6.3.2 Union

[> A union B;  
[> {a,b} union {a,c,d};

Or

[> `union`({a,b},{a,c,d});

6.3.3 Intersection

[> {a,b} intersect {a,c,d};

Or

 `intersect`({a,b},{a,c,d});

6.3.4 Minus

[> {a,b,c,d} minus {a,c,d};

Or

[> `minus`({a,b,c,d},{a,c,d});

[> {a,b} minus {a,b};

6.3.5 Power set

In order to find the power set in maple it will be necessary to import the package that has that command. To import a library we use the with command as follows:

[> restart; with(combinat):
[> A:={p,q,r}; 
[> powerset(A); 

[> powerset({2,k}); 

[> B:={seq(i^2,i=1..5)}; 
[> powerset(B);

6.4 Defining new functions to set theory operations

You can define new functions to use in set theory, because Maple doesn’t contain commands for some set operations.

[> restart; 
[> U:={seq(i,i=1..25)}; # Here U is the universal set 
[> A:={6,12,18,24}; 
[> B:={5,10,15,20,25}; 
[> C:={4,8,12,16,24}; 
[> Complement:=X->U minus X; 
[> Complement(A); 
[> Complement(B);

Following are some complex set theory operations.

  • \((A \cup B)\setminus C\)
[> (A union B)minus C;

  • \((A \cup B)^c\cap (B \cup C)^c\)
[> A union B; 
[> k1:=Complement(%); 
[> k2:=Complement(B union C); 
[> k1 intersect k2;

Or else you can use a single command,

[> Complement(A union B)intersect (Complement(B union C));

6.5 Exercise

Exercise 6.1 Given:

  • \(A = \{1, 2, 4, 7, 9, 11\}\)
  • \(B = \{2, 7, 9, 11, 17, 19\}\)
  • \(C = \{0, 2, 5, 7, 19, 24\}\)

Find:

  1. \(A \cup B\)
  2. \(A \cap B\)
  3. \(A \cap (B \cup C)\)
  4. \(A \cap (B \cap C)\)
  5. \(A \setminus C\)

Exercise 6.2 Create a function to check if two sets are equal. (Hint: use the subset property twice.)

Exercise 6.3 Create a function to find the symmetric difference of two sets, \(A \bigtriangleup B\).

Definition 6.1 The symmetric difference is equivalent to the union of both relative complements, that is: \(A \bigtriangleup B = ( A \setminus B ) \cup ( B \setminus A )\)

Test functions 6.2 and 6.3 with

  • \(A = \{1, 3, 5, 7\}\)
  • \(B = \{2, 4, 5, 6\}\)
  • \(P = \{1, 2, 3, 5, 6, 7\}\)
  • \(Q = \{2, 4, 5, 6\}\)

Exercise 6.4

  1. Generate the set of integers from 1 to 50.
  2. Generate the set of the first 25 powers of 2.
  3. Let K be the set of numbers from 1 to 1100 that are divisible by 11. Find K.