A Stereographic Projection

• Stereographic Projection plane \(\mathbb{R}\) and the 1-sphere minus a point
  The 1-sphere \(S^1\) is the set of points \((x,y,z) \in \mathbb{R}^3\) such that \(x^2 + y^2 + z^2 = 1\). \[S^1:=\{(x,y): ||(x,y)||=1\}\]

Let \(S^1 \setminus \{N\}\) denote the 1-sphere minus (circle) its north pole, i.e., the point \((0,1)\).

There exists a homeomorphism \(\varphi : S^1 \setminus \{N\} \to \mathbb{R}\), which can be described as follows. In coordinates, this map is precisely \[\varphi(x,y) = \frac{x}{1-y}\]

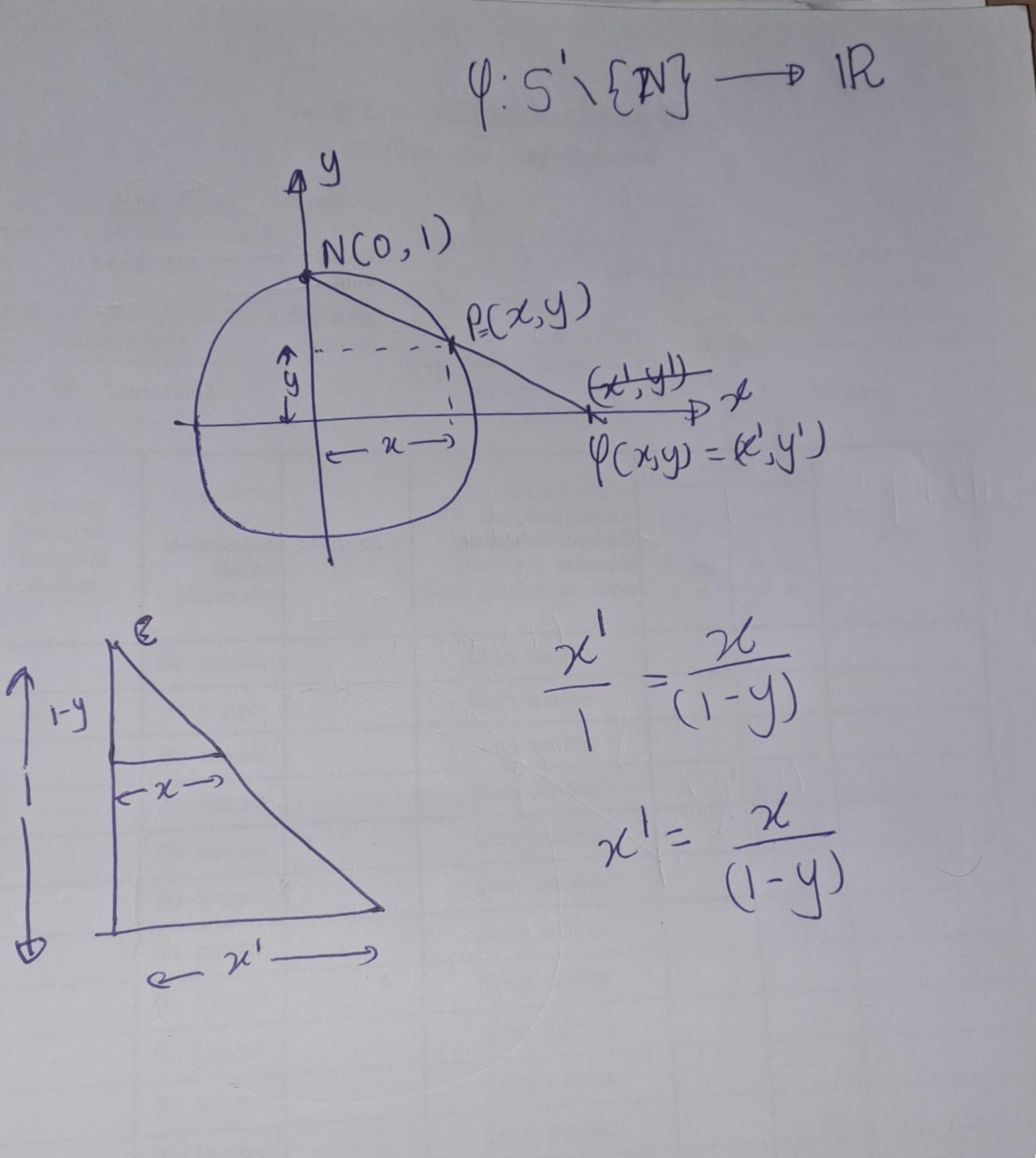
Figure A.1: \(~\)

• Stereographic Projection plane \(\mathbb{R}^2\) and the 2-sphere minus a point
  

Stereographic projection is an important homeomorphism between the plane \(\mathbb{R}^2\) and the 2-sphere minus a point. The 2-sphere \(S^2\) is the set of points \((x,y,z) \in \mathbb{R}^3\) such that \(x^2 + y^2 + z^2 = 1\). Let \(S^2 \setminus \{N\}\) denote the 2-sphere minus its north pole, i.e., the point \((0,0,1)\).

There exists a homeomorphism \(\varphi : S^2 \setminus \{N\} \to \mathbb{R}^2\), which can be described as follows.

For a point \(p \in S^2 \setminus \{N\}\), let \(\varphi(p)\) denote the unique point in \(P\) such that the intersection of the segment \(\overline{Nf(p)}\) and \(S^2\) is \(p\). In coordinates, this map is precisely \[\varphi(x,y,z) = \left(\frac{x}{1-z}, \frac{y}{1-z}\right).\]

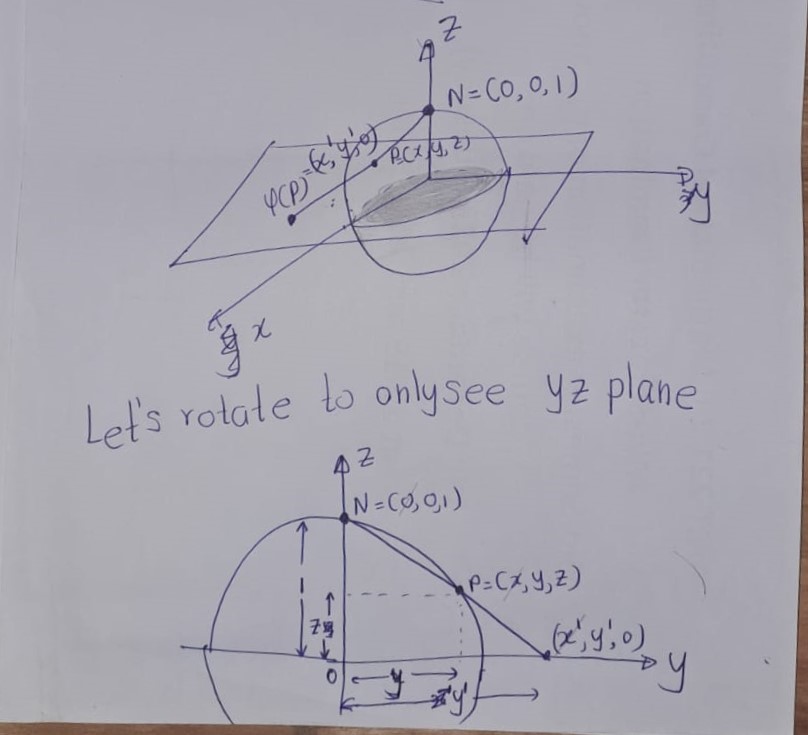
Figure A.2: \(~\)

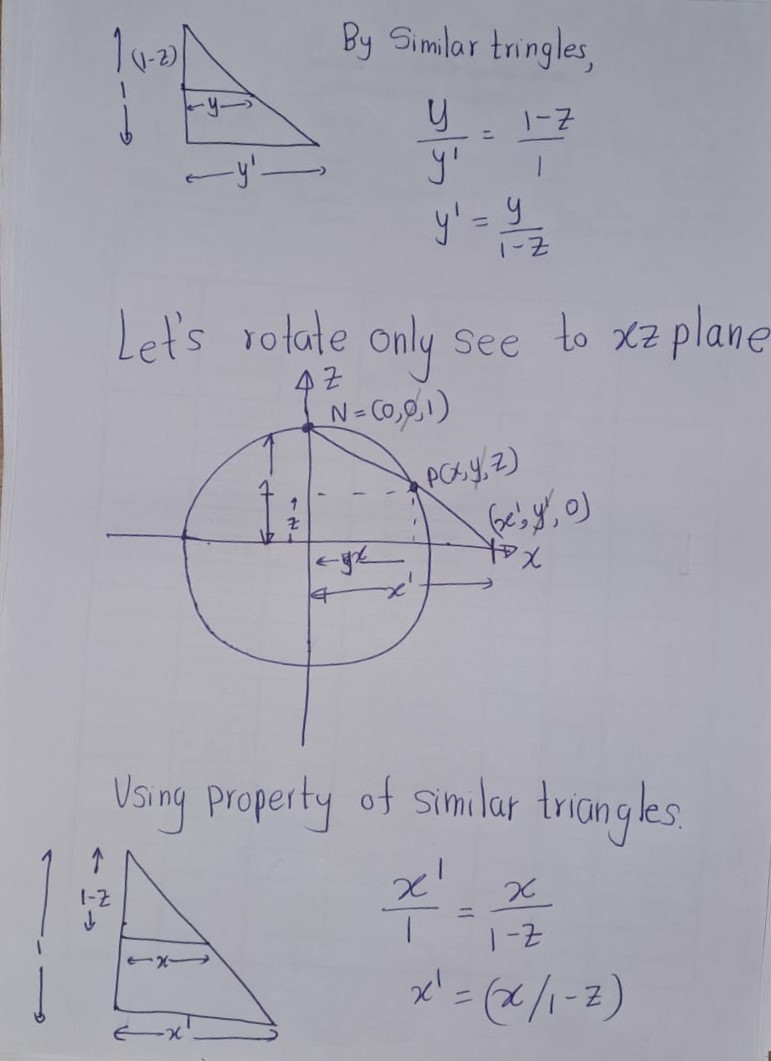
Figure A.3: \(~\)