Chapter 2 Manifolds

2.1 Topological Manifolds

Definition 2.1 Let $(M,\mathcal{T})$ be a topological space with topology $\mathcal{T}$. Then $M$ is called an $n$-dimensional topological manifold, if the following holds:

(TM1): $M$ is Hausdorff.
(TM2): The topology of $M$ has a countable basis.
(TM3): $M$ is locally homeomorphic to $\mathbb{R}^n$, that is, for all $p \in M$ exists an open subset $U \subset M$ with $p \in U$, an open subset $V \subset \mathbb{R}^n$ and a homeomorphism $\varphi : U \rightarrow V$.

Figure 2.1: $~$

Remark. The first two conditions in the definition 2.1 are more of a technical nature and are sometimes neglected. The important fact is that a topological manifold is locally homeomorphic to $\mathbb{R}^n$. Loosely speaking, manifolds look locally like Euclidean space. If the topology on $M$ is induced by a metric, then the first condition is satisfied automatically. If $M$ is given as a subset of $\mathbb{R}^N$ with the subset topology, then both conditions M1 and M2 are satisfied automatically.

Let’s see some examples.

Example 2.1 Euclidean space $M=\mathbb{R}^n$ itself is an $n$-dimensional topological manifold:

(TM1): We know that $\mathbb{R}^n$ is metrc space. Let’s say the metric as $d$. Let $x,y\in \mathbb{R}^n$ with $x\neq y$. Let $r=d(x,y)$. Since $x\neq y$,$r>0$. Let $U_x=B(x,r/2)$ and $U_y=B(y,r/2)$. So, $x\in U_x$ and $y\in U_y$ We need to show that $U_x \cap U_y\neq \emptyset$. We are going to proof by contrdiction. So, asssume the contray, there exist $z\in U_x\cap U_y$. Thus, $d(x,z)<r/2$ and $d(y,z)<r/2$. Then, \[r=d(x,y)\leq d(x,z)+d(z,y)=d(x,z)+d(y,z)<\frac{r}{2}+\frac{r}{2}=r\] This is contradiction. Hence $U_x\cap U_y \neq \emptyset$. Therefore $M=\mathbb{R}^n$ is Hausdorff.
(TM2): Later I will update this part

Problem :(.

(TM3): Let $U=\mathbb{R}^n=M$ and $V=\mathbb{R}^n$ and $\varphi=id$. We can easily tell that idenntity map is bijective. Furthur, we can observe that inverse of identity map is itself and it is well defined. So, Let $U'\subset U=\mathbb{R}^n$ be an open set \[\forall x\in U'\quad id^{-1}(x)=id(x)=x\]. Thus, \[id(U')=id^{-1}(U')=U'.\] Hence, by definition of continuous mapping, $id$ and $id^{-}$ are continuous.

Example 2.2 Let $M \subset \mathbb{R}^n$ be an open subset. Then $M$ is an $n$-dimensional topological manifold.
(TM1), (TM2) Obvious.
(TM3) Holds true with $U = M$, $V = M$ and $x = \text{id}$.

Here Ia m not going to proove this. It is very similar to first example.

Example 2.3 The standard sphere $M = S^n = \{ \underline{y}=(y^0,,.,y^{n}) \in \mathbb{R}^{n+1} : ||\underline{y}|| = 1 \}$ is an $n$-dimensional topological manifold.

(TM1) and (TM2) , since $S^n$ is a subset of $\mathbb{R}^{n+1}$.
(TM3) We construct two homeomorphisms with the help of the stereographic projection. Let $N$ be north pole of the n-sphere, that is $(\underbrace{0,,.,0}_{n~times},1)\in \mathbb{R}^{n+1}$. Let $U_1:=S^n\setminus \{N\}$ and $v_1=\mathbb{R}^{n+1}$. We define

\[\begin{eqnarray} \varphi:U_1&\to & V_1\\ \underline{y} =(y^0,y^1,,.,y^n) & \mapsto & \frac{(y^0,y^1,,.,y^n)}{1-y^{n+1}} \end{eqnarray}\] - Cliam 1: $varphi$ is injective.
Let $(x^0,,.,x^{n}),(y^0,y^1,,.,y^n)\in \mathbb{R}^n$. Suppose that $\varphi(x^0,,.,x^{n})=\varphi(y^0,y^1,,.,y^n)$. \[\begin{eqnarray} \varphi(x^0,,.,x^{n})&=&\varphi(y^0,y^1,,.,y^n)\\ \frac{(x^0,x^1,,.,x^n)}{1-x^{n+1}}&=&\frac{(y^0,y^1,,.,y^n)}{1-y^{n+1}}\\ (y^0, y^1, ,., y^n)(1-x^{n+1}) &=& (x^0, x^1, ,., x^n)(1-y^{n+1})\\ (y^0 - y^0x^{n+1}, y^1 - y^1x^{n+1}, ,., y^n - y^nx^{n+1}) &=& (x^0 - x^0y^{n+1}, x^1 - x^1y^{n+1}, ,., x^n - x^ny^{n+1})\\ y^0(1 - x^{n+1}), y^1(1 - x^{n+1}), ,., y^n (1- y^nx^{n+1}) &=& x^0(1-y^{n+1}), x^1(1 - y^{n+1}), ,., x^n (1- y^{n+1})\\ \end{eqnarray}\] Thus, $y^i(1 - x^{n+1}) = x^i(1 -y^{n+1})$ for all $i = 0, 1, ,., n$. Since $1 - y^{n+1}, 1 - x^{n+1} > 0$, ?

Problem HOW INJECTIVITY COMES:(.

CHECK:(.
- Claim 2: $\varphi$ is surejctive. Surjectivity means that for every $\underline{v} \in V_1 = \mathbb{R}^n$, there exists some $\underline{y} \in U_1$ such that $\varphi(\underline{y}) = \underline{v}$.

So, let $\underline{v} = (v^0, v^1, ,., v^n) \in V_1$. We need to find $\underline{y} = (y^0, y^1, ,., y^n) \in U_1$ such that

\[\frac{(y^0, y^1, ,., y^n)}{1-y^{n+1}} = \underline{v}.\]

We can solve this equation for $\underline{y}$ as follows:

\[\underline{y} = (1-y^{n+1})\underline{v} = \underline{v} - y^{n+1}\underline{v}.\]

We know that $\underline{y} \in U_1 = S^n \setminus \{N\}$, so $y^{n+1} = 1 - \|\underline{y}\|^2$. Substituting this into the equation gives us

\[\underline{y} = \underline{v} - (1 - \|\underline{y}\|^2)\underline{v} = \|\underline{y}\|^2\underline{v}.\]

Solving this equation for $\|\underline{y}\|^2$ gives us

\[\|\underline{y}\|^2 = \frac{\|\underline{v}\|^2}{1 + \|\underline{v}\|^2}.\]

Substituting this back into the equation for $\underline{y}$ gives us

\[\underline{y} = \frac{\underline{v}}{1 + \|\underline{v}\|^2}.\]

This is a well-defined point in $U_1$ for every $\underline{v} \in V_1$, so $\varphi$ is surjective.

Claim: $\varphi$ is continuous.
Note that the inverse map $\phi$ is given by, \[\begin{eqnarray} \phi : V_1 &\rightarrow & U_1\\ \underline{x}= (x^0, x^1, ,. , x^n) &\mapsto & \frac{(x^0,x^1,,.,x^{n-1})}{1 + x^n} \end{eqnarray}\] I will update this proof. I want some to to write rigirs proof:(.

Analogously, we define the homeomorphism, which omits the south pole: Let now $U_2 := S^n \setminus \{S\}$ with $S := ( 0,,. , 0, -1) \in \mathbb{R}^{n+1}$ and $V_2 := \mathbb{R}^n$. Then \[\begin{eqnarray} \varphi : U_2 &\rightarrow & V_2,\\ \underline{y}= (y^0, y^1, ,. , y^n) &\mapsto & \frac{(y^0,y^1,,.,y^n)}{1 + y^n} \end{eqnarray}\]

Therefore, $n$-sphere $S^n$ is an $n$-dimensional topological manifold.

Example 2.4 (Non-Example) We consider $M := \{ (y^1, y^2, y^3) \in \mathbb{R}^3 | (y^1)^2 = (y^2)^2 + (y^3)^2 \}$, the double cone.

Since $M \subset \mathbb{R}^3$, both (i) and (ii) are satisfied.

But $M$ is not a 2-dimensional manifold. Assume it were, then there would exist an open subset $U \subset M$ with $0 \in U$, an open subset $V \subset \mathbb{R}^2$ and a homeomorphism $\varphi : U \rightarrow V$ with $\varphi(0) = 0$. How do we Gruntee that such hormouphsim exsist that maps 0 to 0:( Without losss of generality assume $V = B_r(x(0))$ with $r > 0$. Choose $(p^1,p^2,p^3), (q^1,q^2,q^3) \in U$ with $p^1 > 0$ and $q^1 < 0$. Furthermore, choose a continuous path $c : [0, 1] \rightarrow V$ with $c(0) = x(q_1)$, $c(1) = x(q_2)$ and $c(t) \neq x(0)$ for all $t \in [0, 1]$.

Define the continuous path $\tilde{c} := x^{-1} \circ c : [0, 1] \rightarrow U$. Then $\tilde{c}(0) = q_1$, $\tilde{c}(1) = q_2$, that is, we have $\tilde{c}_1(0) > 0$ while $\tilde{c}_1(1) < 0$. Applying the mean value theorem we find, that there exists a $t \in (0, 1)$ with $\tilde{c}_1(t) = 0$. Then $\tilde{c}(t) = (0, 0, 0)$ and consequently $c(t) = x(\tilde{c}(t)) = x(0)$, which contradicts the choice of $c$. Hence, $M$ is not a 2-dimensional topological manifold.

Definition 2.2 (charts) If $M$ is an $n$-dimensional topological manifold, the homeomorphisms $\varphi : U \to V$ are called charts (or local coordinate systems) of $M$.

Figure 2.2: $~$

After choosing a local coordinate system $\varphi : U \rightarrow V$ every point $p \in U$ is uniquely characterized by its coordinates $(\varphi^1(p), \ldots , \varphi^n(p))$.

Example 2.5 (0-dimesional manifold) In a $0$-dimensional manifold $M$ every point $p \in M$ has an open neighborhood $U$, which is homeomorphic to $R^0 = \{0\}$. Consequently $\{p\} = U$ is an open subset of $M$ for all $p \in M$, that is, $M$ carries the discrete topology. Since there exists a countable basis for the topology on $M$ and the topology is discrete in addition, $M$ has to be countable itself.

Figure 2.3: $~$

Proposition 2.1 A topological space $M$ is a 0-dimensional topological manifold, if and only if $M$ is countable and carries the discrete topology.

Proof.

($\implies$) By definition, a 0-dimensional topological manifold is a topological space where every point has a neighborhood homeomorphic to the 0-dimensional Euclidean space, which is a single point $\{0\}$. This implies that for every point $p \in M$, there exists an open neighborhood $U$ such that $\{p\} = U$. This is exactly the definition of a discrete topology.

Since, there exists a countable basis for the topology on $M$, and every point in $M$ is an open set (i.e., the topology is discrete), then $M$ must be countable. This is because every point in $M$ corresponds to an open set in the basis, and since the basis is countable, $M$ must also be countable.
($\Longleftarrow$) If $M$ carries the discrete topology, then every subset of $M$ is open. In particular, for every point $p \in M$, the set $\{p\}$ is an open set. This means that every point in $M$ has a neighborhood homeomorphic to the 0-dimensional Euclidean space, which is a single point $\{0\}$. This is exactly the definition of a 0-dimensional topological manifold.

If $M$ is countable, then there exists a countable basis for the topology on $M$. Since every point in $M$ is an open set (i.e., the topology is discrete), this basis can be taken to be the set of all singletons $\{p\}$, where $p \in M$.

Therefore, a topological space $M$ is a 0-dimensional topological manifold if and only if $M$ is countable and carries the discrete topology.

Definition 2.3 A topological manifold $M$ is said to be connected, if for every two points $p, q \in M$ there exists a continuous map $c : [0, 1] \to M$ with $c(0) = p$ and $c(1) = q$.

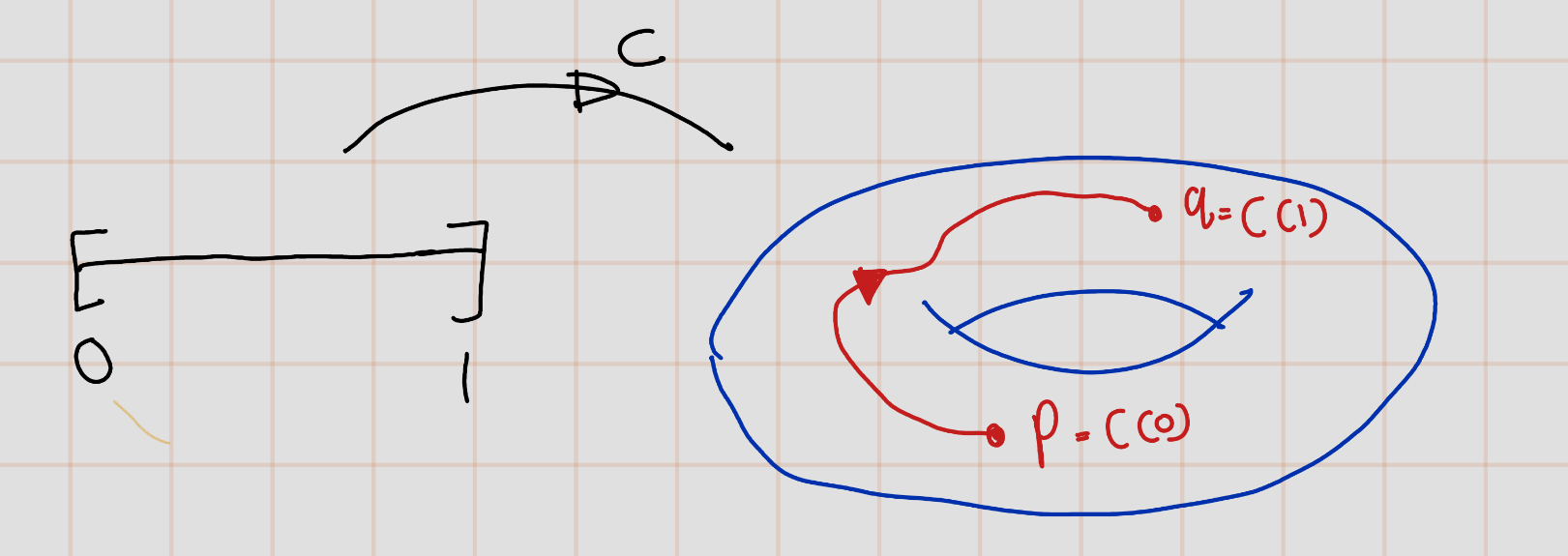
Figure 2.4: $~$

Given two points, there has to be a continuous curve in $M$ which connects both. Usually, in Topology one calls this path-connected, which is in the case of manifolds equivalent to being connected. We do not want to go deeper into this subject at this point.

Remark. Following Proposition every connected 0-dimensional manifold $M$ is given by a single point: $M = \{\text{point}\}$

Proof. Let $M$ be 0-dimesional connected manifold. Then by proposition2.1 $M$ carries the discreate topology. Let $p,q$ be distinct points. (i.e. $p\neq q$). Since $M$ is connected that there exist continuous map $c:[0,1]\to M$ such that $c(0)=p$ and $c(1)=q$.

Let $U=c^{-1}(\{p\})$. Since $\{p\}$ is open in $M$ under discreate toplogy and $c$ is continuous, $U$ is open in $[0,1]$ under subspace topology.

Note that $M\setminus \{p\}$ is sub set of $M$. So, that is open under discreate topology. Since, $c$ is continuous, $V=c^{-1}(M\setminus \{p\})$ is open in $[0,1]$ under subspace topology.

Claim 1: $V \cap U = \emptyset$
\[\begin{eqnarray} V \cap U &=& c^{-1}(M\setminus \{p\}) \bigcap c^{-1}(\{p\})\\ &=& c^{-1}(M\setminus \{p\} \cap \{p\}~~(\text{by Claim 3})\\ &=& c^{-1}(\emptyset)~~(\text{by Claim 4})\\ &=& \emptyset \end{eqnarray}\]
Claim 2: $V \cup U = [0,1]$
\[\begin{eqnarray} V \cup U &=& c^{-1}(M\setminus \{p\}) \bigcup c^{-1}(\{p\})\\ &=& c^{-1}(M\setminus \{p\} \cup \{p\}~~(\text{by Claim 5})\\ &=& c^{-1}(M)\\ &=& [0,1] ~~(\text{by Claim 6}) \end{eqnarray}\]
Claim 3: $c^{-1}(U_1\cap U_2)= c^{-1}(U_1)\cap c^{-1}(U_2)$
- subclaim 3.1 : $c^{-1}(U_1\cap U_2)\subseteq c^{-1}(U_1)\cap c^{-1}(U_2)$
  Let $y\in c^{-1}(U_1\cap U_2)$. Then, $c(y)\in U_1\cap U_2$. Thus, $c(y)\in U_1$ and $c(y)\in U_2$. So, $\in c^{-1}(U_1)$ and $y\in c^{-1}(U_2)$. Thus, $y \in c^{-1}(U_1)\cap c^{-1}(U_2)$. Therefore, $c^{-1}(U_1\cap U_2)\subseteq c^{-1}(U_1)\cap c^{-1}(U_2)$.
- subclaim 3.2 : $c^{-1}(U_1\cap U_2)\supseteq c^{-1}(U_1)\cap c^{-1}(U_2)$
  Let $x\in c^{-1}(U_1)\cap c^{-1}(U_2)$. Then, $x \in c^{-1}(U_1)$ and $x\in c^{-1}(U_2)$. Thus, $c(x)\in U_1$ and $c(x)\in U_2$. So, $x\in c^{-1}(U_1)$ and $x\in c^{-1}(U_2)$. $c(x)\in U_1\cap U_2$. Therefore, $c^{-1}(U_1\cap U_2)\supseteq c^{-1}(U_1)\cap c^{-1}(U_2)$. Therfore $c^{-1}(U_1\cap U_2)= c^{-1}(U_1)\cap c^{-1}(U_2)$.
Claim 4: $c^{-1}(\emptyset)=\emptyset$.
Assume the contray, $c^{-1}(\emptyset)\neq \emptyset$. Then we can choose that $x\in c^{-1}(\emptyset)$. Thus, $c(x)\in\emptyset$. This is a contardiction. Therefore, $c^{-1}(\emptyset)$
Claim 5: $c^{-1}(U_1\cup U_2)= c^{-1}(U_1)\cup c^{-1}(U_2)$.
- subclaim 5.1 : $c^{-1}(U_1\cup U_2)\subseteq c^{-1}(U_1)\cup c^{-1}(U_2)$
  Let $y\in c^{-1}(U_1\cup U_2)$. Then, $c(y)\in U_1\cup U_2$. Thus, $c(y)\in U_1$ or $c(y)\in U_2$. So, $\in c^{-1}(U_1)$ or $y\in c^{-1}(U_2)$. Thus, $y \in c^{-1}(U_1)\cup c^{-1}(U_2)$. Therefore, $c^{-1}(U_1\cup U_2)\subseteq c^{-1}(U_1)\cup c^{-1}(U_2)$.
- subclaim 5.2 : $c^{-1}(U_1\cup U_2)\supseteq c^{-1}(U_1)\cup c^{-1}(U_2)$
  Let $x\in c^{-1}(U_1)\cup c^{-1}(U_2)$. Then, $x \in c^{-1}(U_1)$ or $x\in c^{-1}(U_2)$. Thus, $c(x)\in U_1$ or $c(x)\in U_2$. So, $x\in c^{-1}(U_1)$ or $x\in c^{-1}(U_2)$. $c(x)\in U_1\cup U_2$. Therefore, $c^{-1}(U_1\cup U_2)\supseteq c^{-1}(U_1)\cup c^{-1}(U_2)$. Therfore $c^{-1}(U_1\cup U_2)= c^{-1}(U_1)\cup c^{-1}(U_2)$.
Claim 6: If $c:[0,1]\to M$ be continuous map such that $c(0)=p,c(1)=q$, then $[0,1]=c^{-1}(M)$\ Recall the definition of pre image of $M$. \[c^{-1}(M):=\{x\in M | c(x)\in M\}\]
- Subclaim 6.1: $[0,1]\subseteq c^{-1}(M)$.
  Let $a\in [0,1]$. Then $c(a)\in M$. Thus, $a\in c^{-1}(M)$. Hence, $[0,1]\subseteq c^{-1}(M)$. Thus, $a\in c^{-1}(M)$.
- Subcliam 6.2: $[0,1]\supseteq c^{-1}(M)$.
  Let $b\in c^{-1}(M)$. So, $[0,1]\subseteq c^{-1}(M)$. Thus, $b\in c^{-1}(M)$. Hence $c(b)\in M$. Thus, $b\in [0,1]$.
Claim 7 : $V\neq \emptyset$.
Since $p\neq q$ and $q=c(1)$, then $1\not\in c^{-1}(\{p\})=U$. Thus, $1\in V=[0,1]\setminus U$. Therefore, $V\neq \emptyset$.
Claim 8: $[0,1]$ is connected.
We are going to use proof by contradiction. Suppose that $A,B$ is a separation of $[0,1]$. Let $a \in A$, $b \in B$. Without loss of generality, suppose that $a < b$. Since $a, b \in [0,1]$, and $[0,1]$ is an interval, $[a,b] \subseteq [0,1]$. Let $A' = A \cap [a,b]$ and $B' = B \cap [a,b]$.Then, \[\begin{align*} A' \cup B' &= (A \cap [a,b]) \cup (B \cap [a,b]) \\ &= (A \cup B) \cap [a,b] \quad \text{(Intersection Distributes over Union)} \\ &= [a,b] \quad \text{(Intersection with Subset is Subset)} \end{align*}\] By the definition of a separation, both $A$ and $B$ are closed in $[0,1]$. Hence by Closed Set in Topological Subspace, $A'$ and $B'$ are also closed in $[a,b]$. From Closed Set in Topological Subspace: Corollary, $A'$ and $B'$ are closed in $\mathbb{R}$. Now, since $B' \neq \emptyset$, and $B$ is bounded below (by, for example, $a$), by the Continuum Property $b' := \inf(B')$ exists, and $b' \geq a$. We have that $B'$ is closed in $\mathbb{R}$. Hence from Closure of Real Interval is Closed Real Interval, $b' \in B'$. Since $a \in A'$ and $A \cap B = \emptyset$, it follows that $b' > a$. Now let $A'' = A' \cap [a,b']$. Using the same argument as for $B'$, we have that $a'' = \sup(A'')$ exists, that $a'' \in A''$ and also $a'' < b'$. Now $(a'',b') \cap A' = \emptyset$ or $a''$ would not be an upper bound for $A''$. Similarly, $(a'',b') \cap B' = \emptyset$ or $b'$ would not be a lower bound for $B''$. Thus, $(a'',b') \cap (A' \cup B') = \emptyset$. But since $a < a'' < b' < b$, we also have $(a'',b') \subseteq [a,b]$, and $(a'',b')$ is non-empty. So, there is an element $z \in (a'',b')$, and hence in $[a,b]$, which is not in $A' \cup B'$. This contradicts (1) above, which says that we have $A' \cup B' = [a,b]$. From this contradiction it follows that there can be no such separation $A \mid B$ on the interval $[0,1]$. Therefore, by definition, $[0,1]$ is connected.

By claim 1,2 and 7, $U,V$ are separation of $[0,1]$. This is contartract the the connectedness of $[0,1]$ interval.

Proposition 2.2 Every connected $1$-dimensional topological manifold is homeomorphic to $\mathbb{R}$ or to $S^1$.

Proof. Hard

The only compact,connected topological manifold of dimension $1$ is $S^1$

Theorem 2.1 Let $M$ and $A$ be sets. (Here $A$ is the index set.) For all $\alpha \in A$ assume that $U_\alpha \subset M$ and $V_\alpha \subset \mathbb{R}^n$ are subsets and that $\varphi_\alpha : U_\alpha \rightarrow V_\alpha$ are bijective maps. Suppose the following holds:

$\bigcup_{\alpha \in A} U_\alpha = M$,
$\varphi_\alpha(U_\alpha \cap U_\beta) \subset \mathbb{R}^n$ is open for all $\alpha, \beta \in A$ and
$\varphi_\beta \circ \varphi_\alpha^{-1} : \varphi_\alpha(U_\alpha \cap U_\beta) \rightarrow \varphi_\beta(U_\alpha \cap U_\beta)$ is continuous for all $\alpha, \beta \in A$.

Then $M$ carries a unique topology for which all $U_\alpha$ are open sets and all $\varphi_\alpha$ are homeomorphisms.

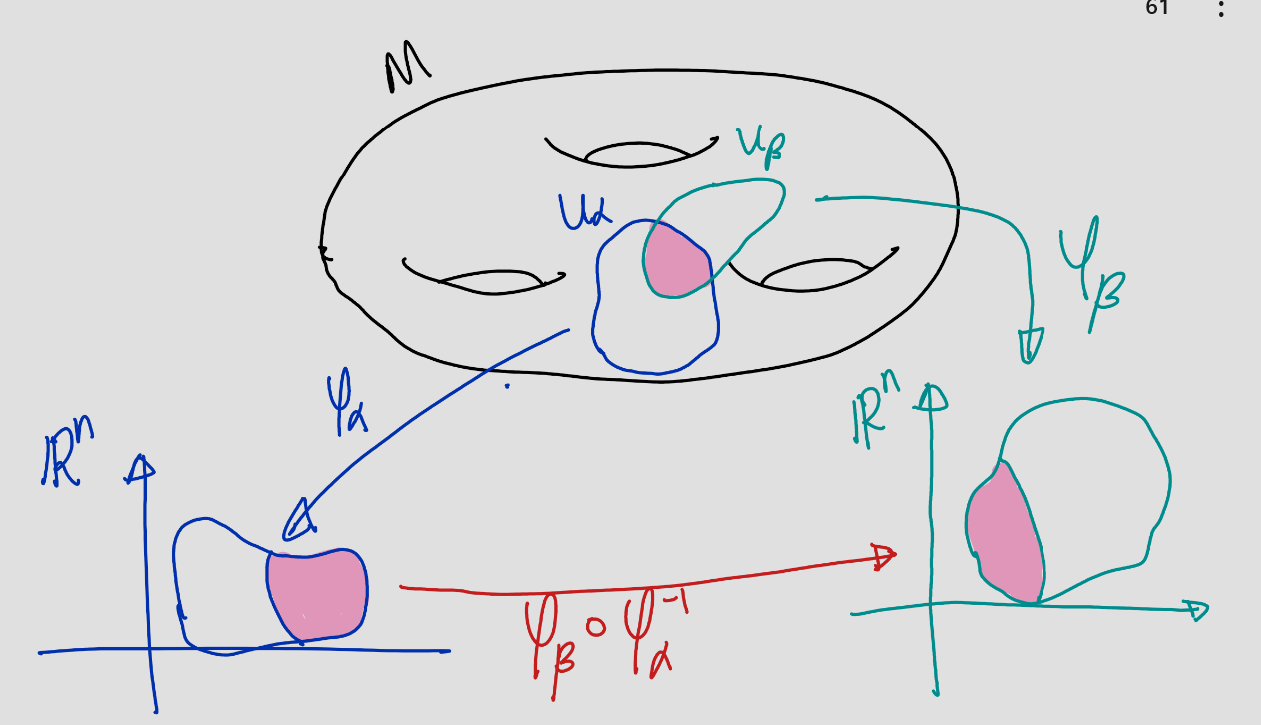
Figure 2.5: $~$

Proof. We first show uniqueness:
Let $\mathcal{T}$ be a topology on $M$ containing the $U_\alpha$ and such that the $\varphi_\alpha$ are homeomorphisms. If $W \in \mathcal{T}$, then also $W \cap U_\alpha \in \mathcal{T}$ and $\varphi_\alpha(W \cap U_\alpha)$ is open for all $\alpha \in A$. Conversely, if $W \subset M$ is a subset such that $\varphi_\alpha(W \cap U_\alpha) \subset \mathbb{R}^n$ is open for all $\alpha \in A$, then $W \cap U_\alpha$ is also open in $U_\alpha$ for all $\alpha$. Since $U_\alpha$ is open in $M$, the set $W \cap U_\alpha$ is open in $M$. By (i), $W = \bigcup_{\alpha \in A} (W \cap U_\alpha)$ is also open in $M$. We have shown that $W \in \mathcal{T}$ if and only if $\varphi_\alpha(W \cap U_\alpha)$ is open in $\mathbb{R}^n$ for all $\alpha$, \[\mathcal{T} = \{W \subset M :~ \varphi_\alpha(W \cap U_\alpha) \subset \mathbb{R}^n \text{ is open for all } \alpha \in A\}\].

Example 2.6 (Real-projective space.) We define the real-projective space by \[ M = \mathbb{RP}^n := \mathbb{P}(\mathbb{R}^{n+1}) := \{ L \subset \mathbb{R}^{n+1} \mid L \text{ is a one-dimensional vector subspace} \}. \]

We will use Theorem 2.1 to equip $\mathbb{RP}^n$ with the structure of an $n$-dimensional topological manifold. Let’s set \[ A := \{ \text{affine-linear embeddings } \alpha : \mathbb{R}^n \to \mathbb{R}^{n+1} \text{ with } 0 \notin \alpha(\mathbb{R}^n) \}. \]

Since $\alpha$ is affine-linear, there exist a matrix $B \in \text{M}_{(n+1) \times n} (\mathbb{R})$ and a vector $c \in \mathbb{R}^{n+1}$ such that \[ \alpha(x) = Bx + c \quad \text{for all } x \in \mathbb{R}^n. \]

As $\alpha$ is an embedding, $B$ has maximal rank, i.e., $\text{rank}(B) = n$.

Consequently, $\alpha(\mathbb{R}^n)$ is an affine-linear hyperplane. Let’s set \[ U_\alpha := \{ L \in \mathbb{RP}^n \mid L \cap \alpha(\mathbb{R}^n) \neq \varnothing \}. \]

For $L \in U_\alpha$, the space $L \cap \alpha(\mathbb{R}^n)$ consists of exactly one point, because otherwise we would have $L \subset \alpha(\mathbb{R}^n)$ and hence $0 \in \alpha(\mathbb{R}^n)$, which is a contradiction. Moreover, we have \[ \mathbb{RP}^n \setminus U_\alpha = \{ L \mid L \subset B(\mathbb{R}^n) \text{ is a one-dimensional subspace} \} \] where $\alpha(x) = Bx + c$. For $\alpha \in A$, let’s set $V_\alpha := \mathbb{R}^n$ and define \[ \varphi_\alpha : U_\alpha \to V_\alpha, \quad \varphi_\alpha(L) := \alpha^{-1}(L \cap \alpha(\mathbb{R}^n)). \]

Then $x_\alpha$ is a bijective map, and we have \[ \varphi_\alpha^{-1}(v) = R \cdot \alpha(v). \]