Manifolds
2024-03-12
Chapter 1 Basic Theroms and Definitions
Definition 1.1 (Topology) A topology on a set \(X\) is a collection \(\mathcal{T}\) of subsets of \(X\) such that
(T1) \(\phi\) and \(X\) are in \(\mathcal{T}\);
(T2) Any union of subsets in \(\mathcal{T}\) is in \(\mathcal{T}\);
(T3) The finite intersection of subsets in \(\mathcal{T}\) is in \(\mathcal{T}\).
A set \(X\) with a topology \(\mathcal{T}\) is called a topological space. Denoted by \((X,\mathcal{T})\). An element of \(\mathcal{T}\) is called an open set.
Definition 1.2 A subset \(U \subset M\) is referred to as open in \(M\) if \(U \in \mathcal{T}\). A subset \(A \subset M\) is termed closed if \(M \setminus A \in \mathcal{T}\).
Definition 1.3 (Continuity) If both \((M, \mathcal{T}_M)\) and \((N, \mathcal{T}_N)\) are topological spaces, a map \(f : M \rightarrow N\) is termed continuous if \[f^{-1}(V) \in \mathcal{T}_M \text{ for all } V \in \mathcal{T}_N\]. In other words, the preimages of open sets must be open.
Definition 1.4 (Homemorphism) A map \(f : M \rightarrow N\) between two topological spaces is called homemorphism if it has following propoties. - \(f\) is a bijection, - \(f\) is continuous, - the inverse function \(f^{-1}\) is continuous.
Two topological spaces \(M\) and \(N\) are called homeomorphic if there exists a homeomorphism between them.
Definition 1.5 (Hausdorff Space) A topological space \((X,\mathcal{T})\) is called a Hausdorff space if
(H1) \(\forall x,y \in X\) such that \(x \neq y\), \(\exists U_x, U_y \in \mathcal{T}\) such that \(x \in U_x\), \(y \in U_y\), and \(U_x \cap U_y = \emptyset\).
i.e., for every pair of distinct points \(x, y\) in \(X\), there are disjoint neighborhoods \(U_x\) and \(U_y\) of \(x\) and \(y\) respectively.
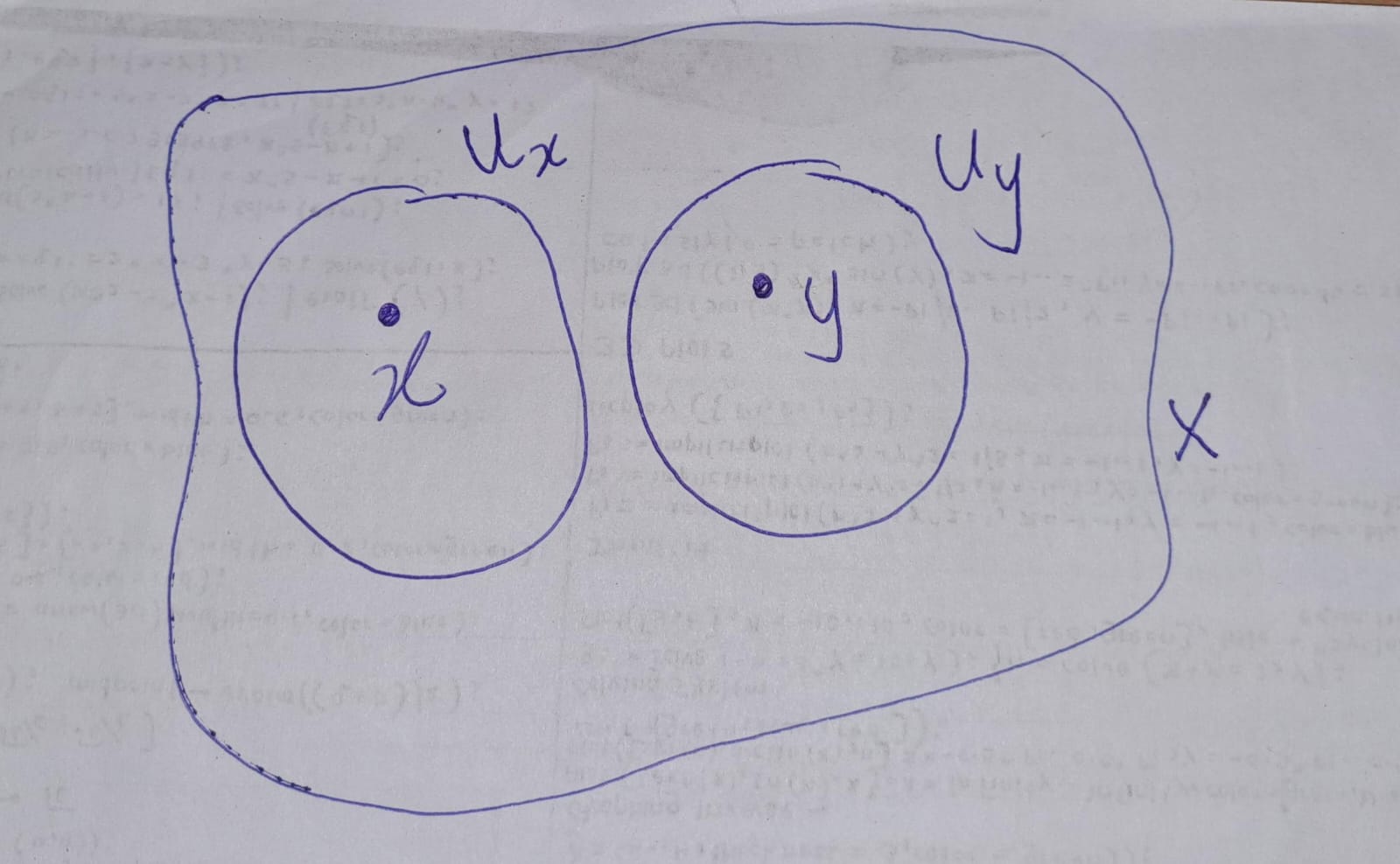
Figure 1.1: \(~\)
Definition 1.6 (Countability) A space \(X\) is said to have a countable basis at the point \(x\) if there is a countable collection \(\{U_n\}_{n\in\mathbb{Z}^+}\) of neighborhoods of \(x\) such that any neighborhood \(U\) of \(x\) contains at least one of the sets \(U_n\). A space \(X\) that has a countable basis at each of its points is said to satisfy the first countability axiom.
Definition 1.7 If \(X\) is a space, a point \(x\) of \(X\) is said to be an isolated point of \(X\) if the one-point set \(\{x\}\) is open in \(X\).