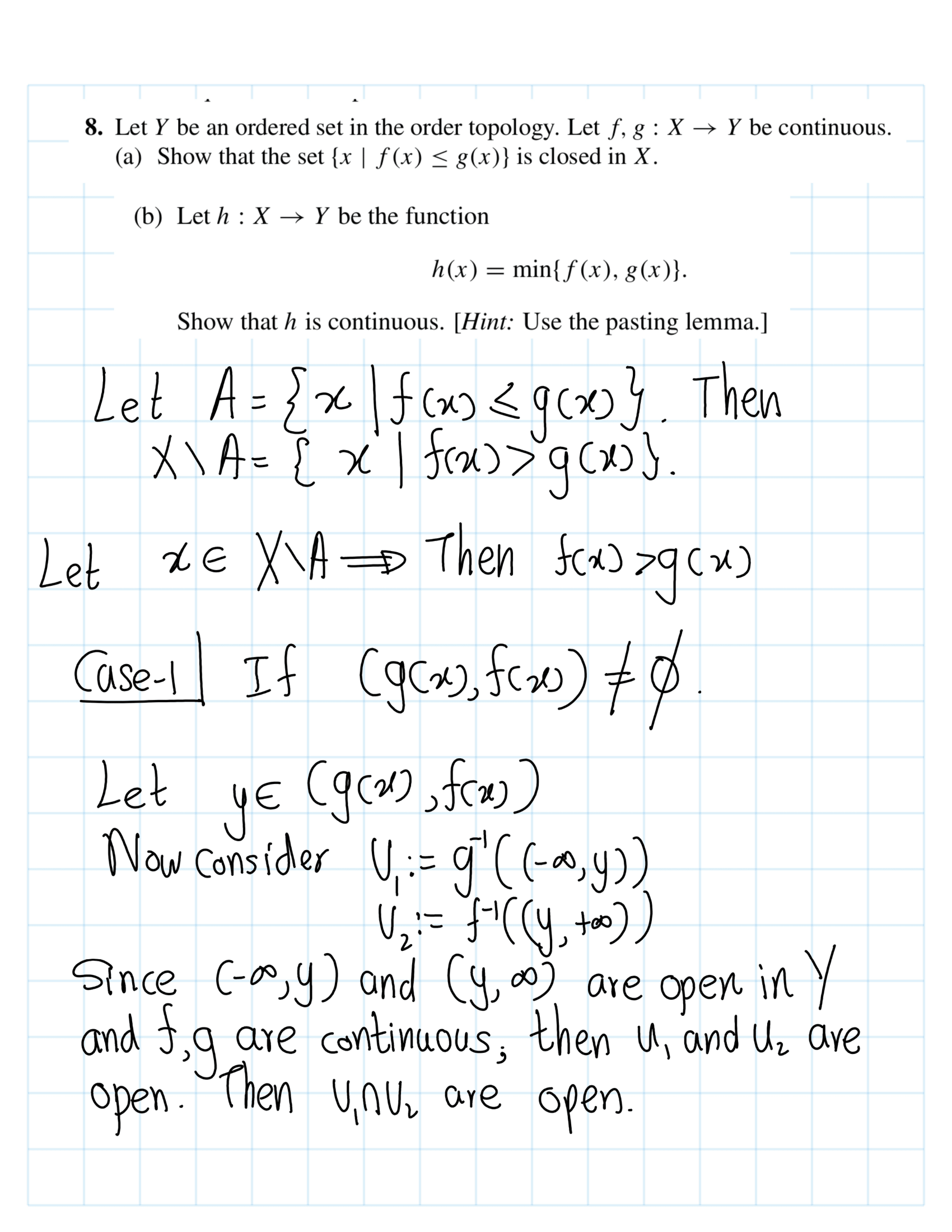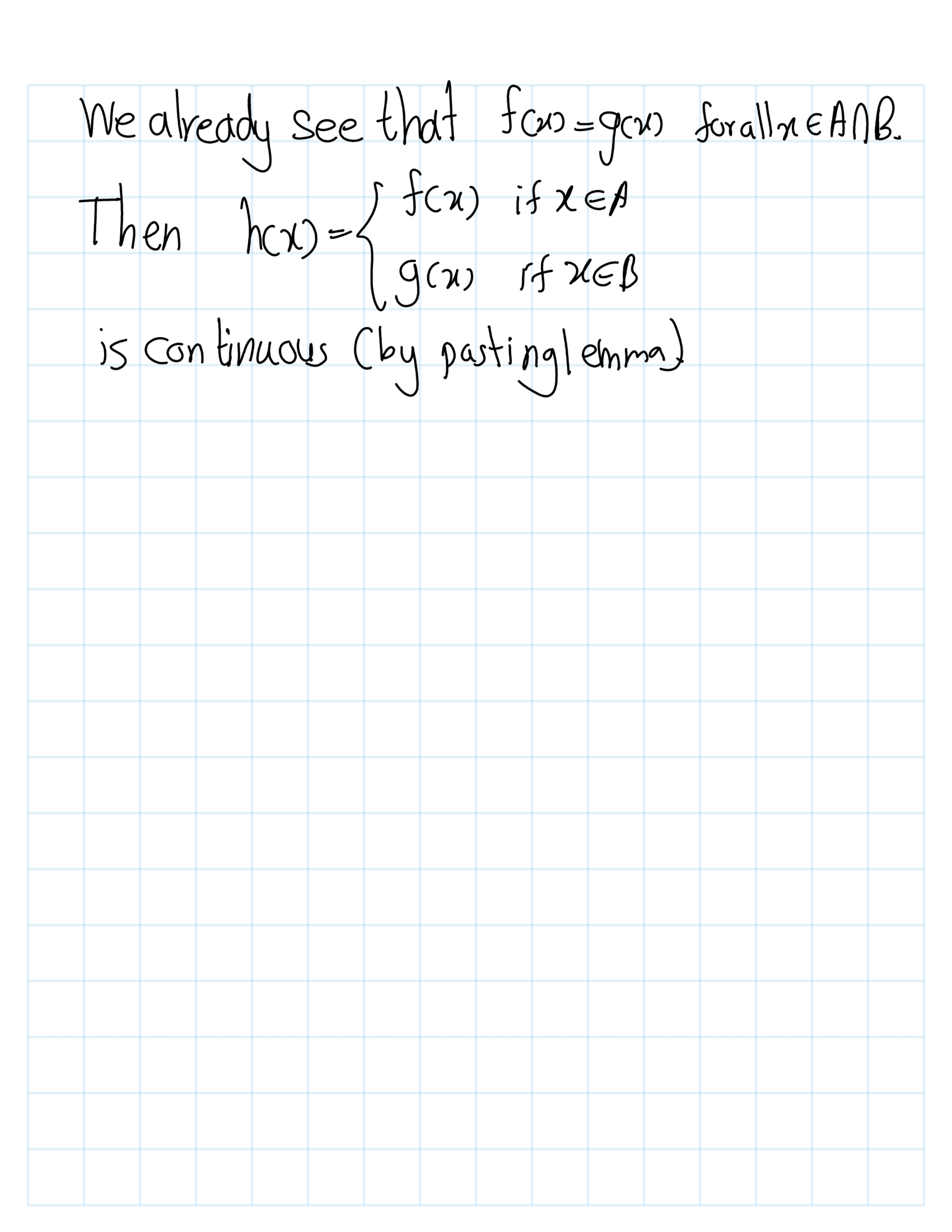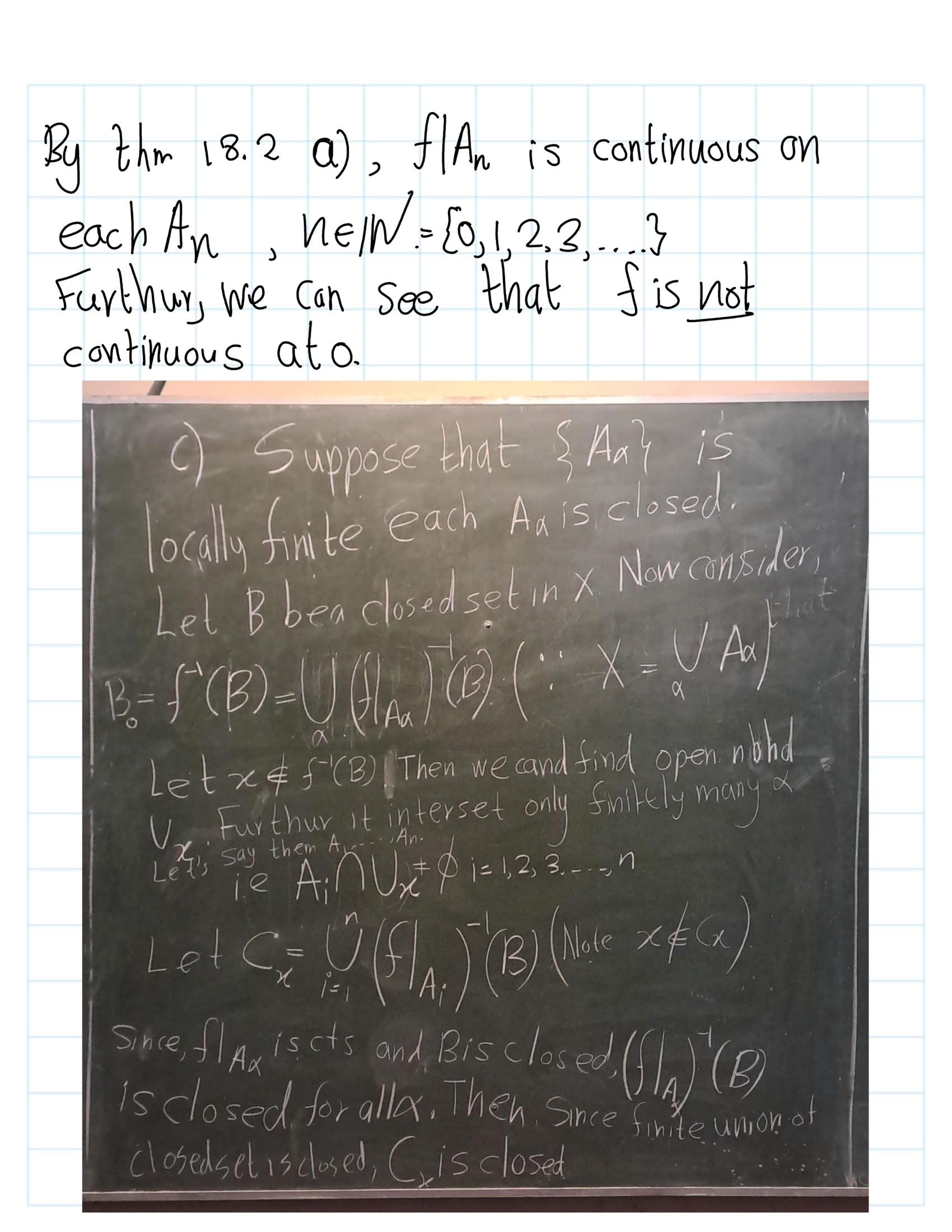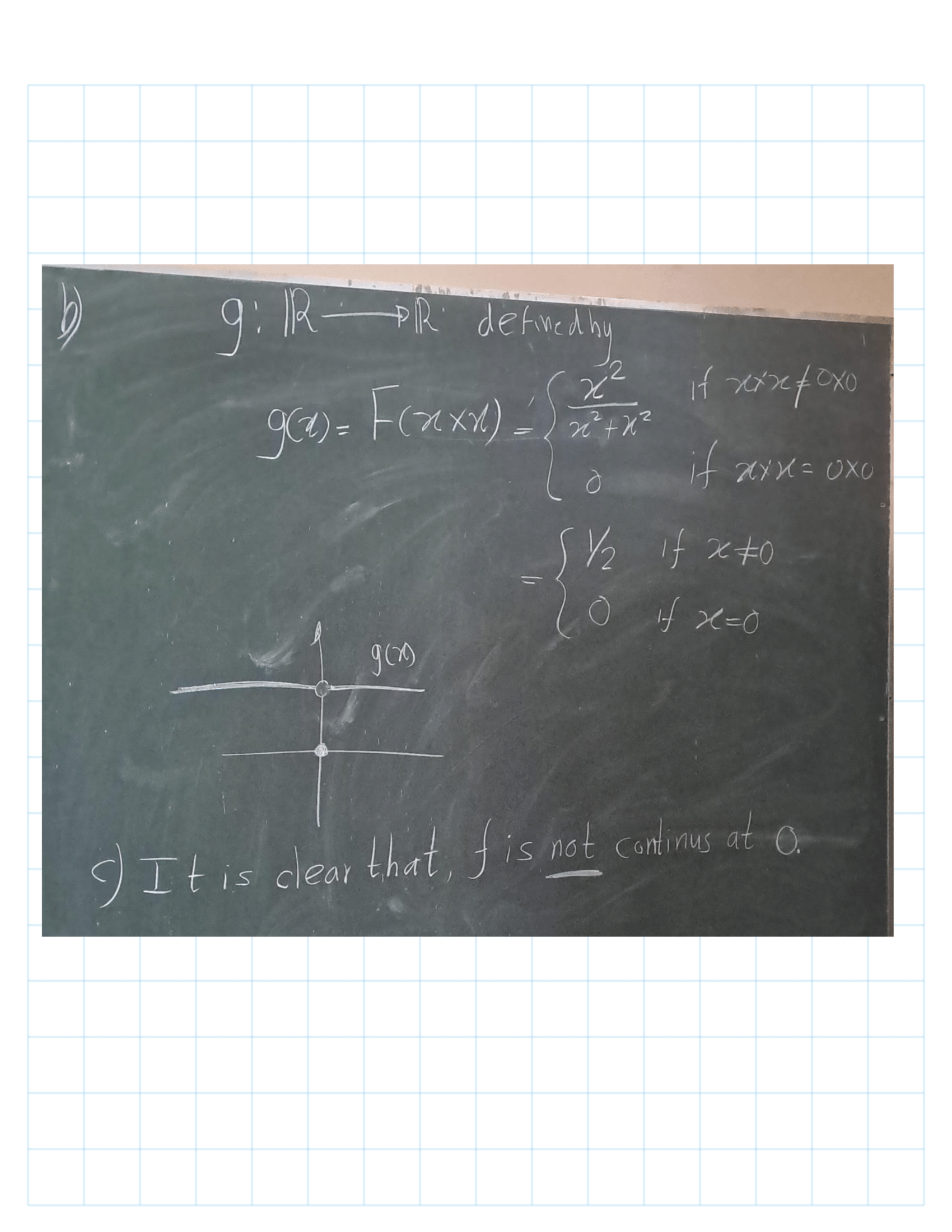Chapter 4 Exercises

4.1 Section 13 in Munkrees book

Exercise 4.1 (Mun 2.13.1) Let $X$ be a topological space; let $A$ be a subset of $X$. Suppose that for each $x \in A$ there is an open set $U$ containing $x$ such that $U \subset A$. Show that $A$ is open in $X$.

Proof. Let $X$ be a topological space. Let $A$ be a subset of $X$. Suppose that for each $x \in A$. Then $U_x$ be the open set that, \[x\in U_x\subseteq A\] Now consider, \[U:=\bigcup_{x\in A}U_x.\] Note that $U$ is open. By defintion of toplogy. Furthur, $A=U$. Hence, $A$ is open set.

Exercise 4.2 (Mun 2.13.3) Consider the nine topologies on the set X = {a, b, c} indicated in Example 1 of §12. Compare them; that is, for each pair of topologies, determine whether they are comparable, and if so, which is the finer.

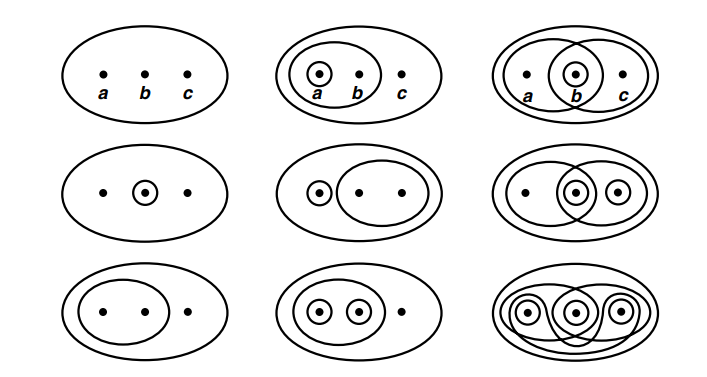
Figure 4.1: $~$

These topologies can be listed as follows, \[\begin{align*} \mathcal{T}_1 &= \{\emptyset, X\}, \\ \mathcal{T}_2 &= \{\emptyset, \{a\}, \{a, b\}, X\}, \\ \mathcal{T}_3 &= \{\emptyset, \{b\}, \{a, b\}, \{b, c\}, X\}, \\ \mathcal{T}_4 &= \{\emptyset, \{b\}, X\}, \\ \mathcal{T}_5 &= \{\emptyset, \{a\}, \{b, c\}, X\}, \\ \mathcal{T}_6 &= \{\emptyset, \{b\}, \{c\}, \{a, b\}, \{b, c\}, X\}, \\ \mathcal{T}_7 &= \{\emptyset, \{a, b\}, X\}, \\ \mathcal{T}_8 &= \{\emptyset, \{a\}, \{b\}, \{a, b\}, X\}, \\ \mathcal{T}_9 &= \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, X\}. \end{align*}\] We can get following observations. - $\mathcal{T}_1$ is coarser than any other topology, - $\mathcal{T}_9$ is finer than any other topology. - $\mathcal{T}_7 \subset \mathcal{T}_2 \subset \mathcal{T}_8$ - $\mathcal{T}_4 \subset \mathcal{T}_3 \subset \mathcal{T}_6$ - $\mathcal{T}_7 \subset \mathcal{T}_3 \subset \mathcal{T}_6$ - $\mathcal{T}_4 \subset \mathcal{T}_8$.

Exercise 4.3 Show that the collection $\mathcal{T}_c$ given in Example 4 of §12 (in Munkrees book) is a topology on the set $X$. Is the collection \[\mathcal{T}_{\infty} = \{U | X - U \text{ is infinite or empty or all of } X\}\] a topology on $X$?

Proof. (Proof of $\mathcal{T}_c$ is toplogy.) Recall: $\mathcal{T}_c$ is the collection of all subsets $U$ of $X$ such that $X \setminus U$ is either countable or is all of $X$.

$\emptyset\in \mathcal{T}_c$. (Beacuse $X\setminus \emptyset=X$)
$X \in \mathcal{T}_c$. (Beacuse $X\setminus X=\emptyset$ is countable)
So, $\emptyset$ and $X$ are both in $\mathcal{T}_c$.
Let $\{U_\alpha\}_{\alpha \in J}$ be a family of sets in $\mathcal{T}_c$. Then \[X \setminus \bigcup_{\alpha \in J} U_\alpha = \bigcap_{\alpha \in J} (X \setminus U_\alpha)\quad\text{ (By De Moragons Law)}\] is an intersection of countable sets, hence countable.
If $U_1, \ldots, U_n$ are elements in $\mathcal{T}_c$, then \[X \setminus \bigcap_{i=1}^{n} U_i = \bigcup_{i=1}^{n} (X \setminus U_i)quad\text{ (By De Moragons Law)}\] is countable being a union of countable sets. It follows that $\mathcal{T}_c$ is a topology on $X$.

Note that $\mathcal{T}_\infty$ is in general not a topology on $X$.

For example, let $X = \mathbb{R}$,
$U_1 = (-\infty, 0)$ and $U_2 = (0, \infty)$.
Then $U_1$ and $U_2$ are in $\mathcal{T}_\infty$ but $U_1 \cup U_2 = \mathbb{R} \setminus \{0\}$ is not.

Exercise 4.4 (Mun 2.13.4)

If $\{\mathcal{T}_\alpha\}$ is a family of topologies on $X$, show that $\bigcap \mathcal{T}_\alpha$ is a topology on $X$. Is $\bigcup \mathcal{T}_\alpha$ a topology on $X$?
Let $\{\mathcal{T}_\alpha\}$ be a family of topologies on $X$. Show that there is a unique smallest topology on $X$ containing all the collections $\mathcal{T}_\alpha$, and a unique largest topology contained in all $\mathcal{T}_\alpha$.
If $X = \{a, b, c\}$, let \[\begin{align*} \mathcal{T}_1 &= \{\emptyset, X,\{a\},\{a, b\}\} \text{ and } \\ \mathcal{T}_2 &= \{\emptyset, X,\{a\},\{b, c\}\}. \end{align*}\] Find the smallest topology containing $\mathcal{T}_1$ and $\mathcal{T}_2$, and the largest topology contained in $\mathcal{T}_1$ and $\mathcal{T}_2$.

Solution:

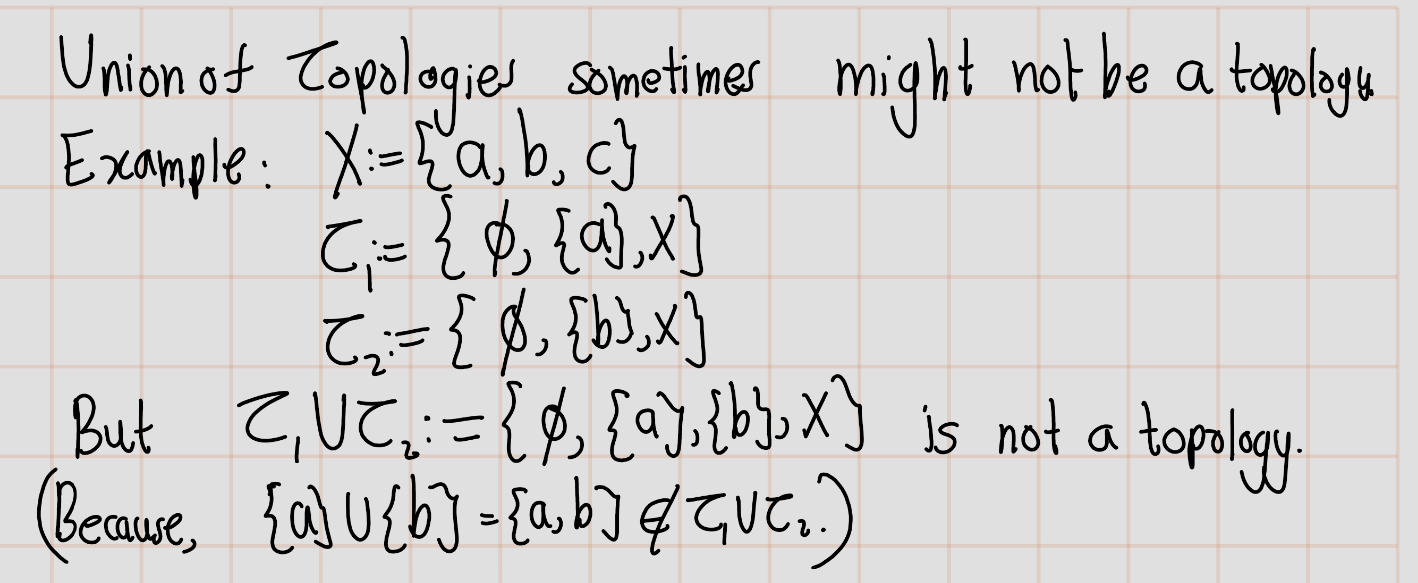
Let Let $\{\mathcal{T}_\alpha\}$ be a family of topologies on $X$. Let $\mathcal{F}:\{\mathcal{T}_\beta: \mathcal{T}_\beta\supseteq \bigcup \mathcal{T}_\alpha\}$ be family of topology that contain $\bigcup\mathcal{T}_\alpha$.

Exercise 4.5 (Mun 2.13.5) Show that if $A$ is a basis for a topology on $X$, then the topology generated by $A$ equals the intersection of all topologies on $X$ that contain $A$. Prove the same if $A$ is a subbasis.

Exercise 4.6 (Mun 2.13.6) Show that the topologies of $\mathbb{R}_l$ and $\mathbb{R}_K$ are not comparable.

Exercise 4.7 (Mun 2.13.7) Consider the following topologies on $\mathbb{R}$: \[\begin{eqnarray} \mathcal{T}_1 &:=& \text{ the standard topology}\\ \mathcal{T}_2 &:=& \text{ the topology of $\mathbb{R}_K$,}\\ \mathcal{T}_3 &:=& \text{ the finite complement topology,}\\ \mathcal{T}_4 &:=& \text{ the upper limit topology, having all sets $(a, b]$ as basis,}\\ \mathcal{T}_5 &:=& \text{ the topology having all sets $(-\infty, a) = \{x | x < a\}$ as basis.} \end{eqnarray}\]

Determine, for each of these topologies, which of the others it contains.

Exercise 4.8 (Mun 2.13.8)

Apply Lemma 13.2 to show that the countable collection \[ \mathcal{B} = \{(a, b) | a < b, a \text{ and } b \text{ rational}\} \] is a basis that generates the standard topology on $\mathbb{R}$.
Show that the collection \[ \mathcal{C} = \{[a, b) | a < b, a \text{ and } b \text{ rational}\} \] is a basis that generates a topology different from the lower limit topology on $\mathbb{R}$. \end{enumerate}

4.2 Section 16 in Munkress Book

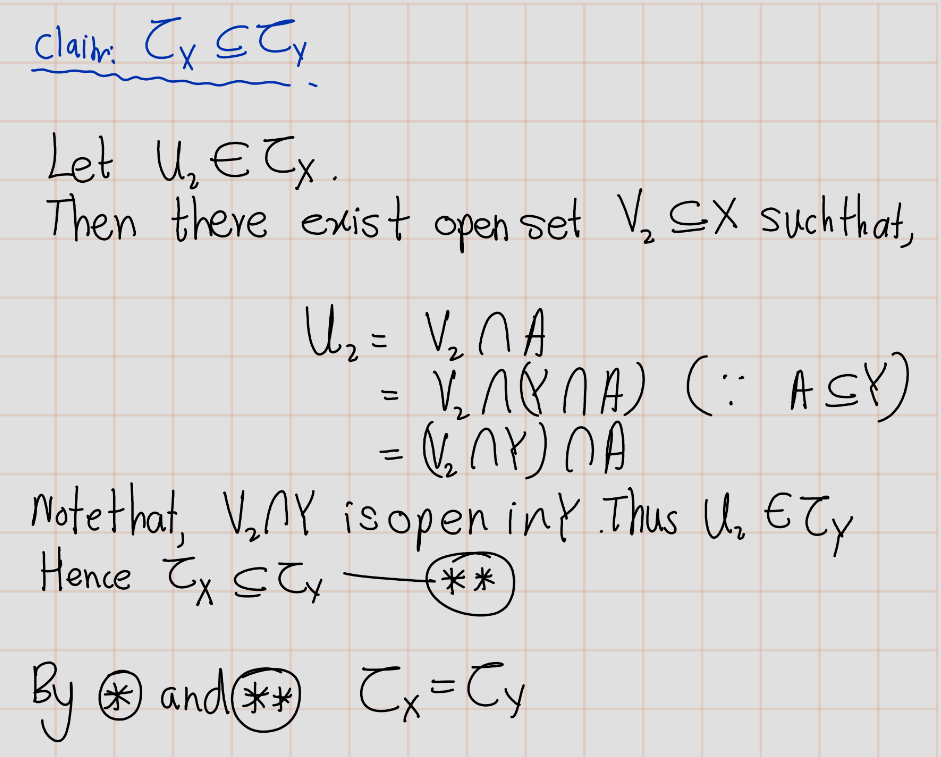
Exercise 4.9 (Mun 2.16.2) Show that if $Y$ is a subspace of $X$, and $A$ is a subset of $Y$ , then the topology $A$ inherits as a subspace of $Y$ is the same as the topology it inherits as a subspace of $X$.

Solution: Let’s denote the topology on $X$ as $\mathcal{T}_X$, the topology on $Y$ as $\mathcal{T}_Y$, and the topology on $A$ as $\mathcal{T}_A$.

We know that $Y$ is a subspace of $X$, so the topology $\mathcal{T}_Y$ that $Y$ inherits from $X$ is $\mathcal{T}_Y = \{ Y \cap U : U \in \mathcal{T}_X \}$.

Similarly, $A$ is a subset of $Y$, so the topology $\mathcal{T}_A$ that $A$ inherits from $Y$ is $\mathcal{T}_A = \{ A \cap V : V \in \mathcal{T}_Y \}$.

Substituting $\mathcal{T}_Y$ into the equation for $\mathcal{T}_A$, we get $\mathcal{T}_A = \{ A \cap (Y \cap U) : U \in \mathcal{T}_X \}$.

Since $A$ is a subset of $Y$, $A \cap Y = A$. So, $\mathcal{T}_A = \{ A \cap U : U \in \mathcal{T}_X \}$.

This is exactly the topology that $A$ would inherit as a subspace of $X$. Therefore, the topology $A$ inherits as a subspace of $Y$ is the same as the topology it inherits as a subspace of $X$.

Exercise 4.10 (Mun 2.16.2) If $\mathcal{T}$ and $\mathcal{T}$ are topologies on $X$ and $\mathcal{T}$ is strictly finer than $\mathcal{T}$ , what can you say about the corresponding subspace topologies on the subset $Y$ of $X$?

Solution:

Exercise 4.11 (Mun 2.16.3) Consider the set $Y = [−1, 1]$ as a subspace of $\mathbb{R}$. Which of the following sets are open in $Y$ ? Which are open in $\mathbb{R}$? \[\begin{align} A &= \{ x \mid \frac{1}{2} < |x| < 1 \}\\ B &= \{ x \mid \frac{1}{2} < |x| \leq 1 \} \\ C &= \{ x \mid \frac{1}{2} \leq |x| < 1 \}\\ D &= \{ x \mid \frac{1}{2} \leq |x| \leq 1 \}\\ E &= \{ x \mid 0 < |x| < 1 \text{ and } \frac{1}{x} \notin \mathbb{Z}^+ \} \end{align}\]

Solution:

Exercise 4.12 A map $f : X \to Y$. We say that $f$ is an open map if, for every open set $U$ in $X$, the set $f(U)$ is open in $Y$. Show that the projections $\pi_1 : X \times Y \to X$ and $\pi_2 : X \times Y \to Y$ are open maps. ``

Exercise 4.13 Let $X$ and $X^\prime$ denote a single set in the topologies $\mathcal{T}$ and $\mathcal{T}^\prime$ , respectively; let $Y$ and $Y'$ denote a single set in the topologies $\mathcal{U}$ and $\mathcal{U}^\prime$, respectively. Assume these sets are nonempty.

Show that if $\mathcal{T}' \supset \mathcal{T}$ and $\mathcal{U}'\supset \mathcal{U}$, then the product topology on $X'\times Y'$ is finer than the product topology on $X \times Y$.
Does the converse of a. hold? Justify your answer

Exercise 4.14 (Mun 2.16.7) Show that the countable collection \[\{(a, b) \times (c, d) | a < b \text{ and } c < d, \text{ and } a, b, c, d \text{ are rational}\}\] is a basis for $\mathbb{R}^2$.”

Exercise 4.15 Let $X$ be an ordered set. If $Y$ is a proper subset of $X$ that is convex in $X$, does it follow that $Y$ is an interval or a ray in $X$?

Exercise 4.16 If $L$ is a straight line in the plane, describe the topology $L$ inherits as a subspace of $\mathbb{R}_l \times \mathbb{R}$ and as a subspace of $\mathbb{R}_l \times \mathbb{R}_l$. In each case it is a familiar topology.

Exercise 4.17 Show that the dictionary order topology on the set $\mathbb{R} \times \mathbb{R}$ is the same as the product topology $\mathbb{R}_d \times \mathbb{R}$, where $\mathbb{R}_d$ denotes $\mathbb{R}$ in the discrete topology. Compare this topology with the standard topology on $\mathbb{R}^2$.

\[\mathbb{R}^2_{dictionary}:=\mathbb{R}_{discrete }\times \mathbb{R}_{standard}\]

Proof. Let $\{a\} \times (c,d)$ be a basis element in product toplogy $\mathbb{R}_d \times \mathbb{R}$. Let $a\times x\in \{a\} \times (c,d)$ obsereve that \[a\times x\in \{a\} \times (c,d) = (a\times c,a\times d)\] and $(a\times c,a\times d)$ is basis element of order topology $\mathbb{R}^2$. Thus by lemma 1.4, order toplogy in $\mathbb{R}^2$ is finer than the product toplogy $\mathbb{R}_d \times \mathbb{R}$.

Now suppose that $(p\times q, r \times s)$ be a basis elemenet in order toplogy on $\mathbb{R}^2$.

If $p<x$, define $l=y−1$ and if $p=x$ define $l=r$. In either case we know that $(p\times q)<(x\times l)<(x\times y)$.
If $x<r$ define $t=y+1$ and if $x=r$ define $t=s$. In either case we know that $(x\times y)<(x\times t)<(q \times s)$.

See figure 1.12 So \[(x,y) \in \{x\} \times (l,t) \subseteq (p \times q, r \times s).\] Thus by lemma 1.4, product toplogy $\mathbb{R}_d \times \mathbb{R}$ is finer than order toplogy in $\mathbb{R}^2$.

Therefore, \[\mathbb{R}^2_{dictionary}=\mathbb{R}_{discrete }\times \mathbb{R}_{standard}\]

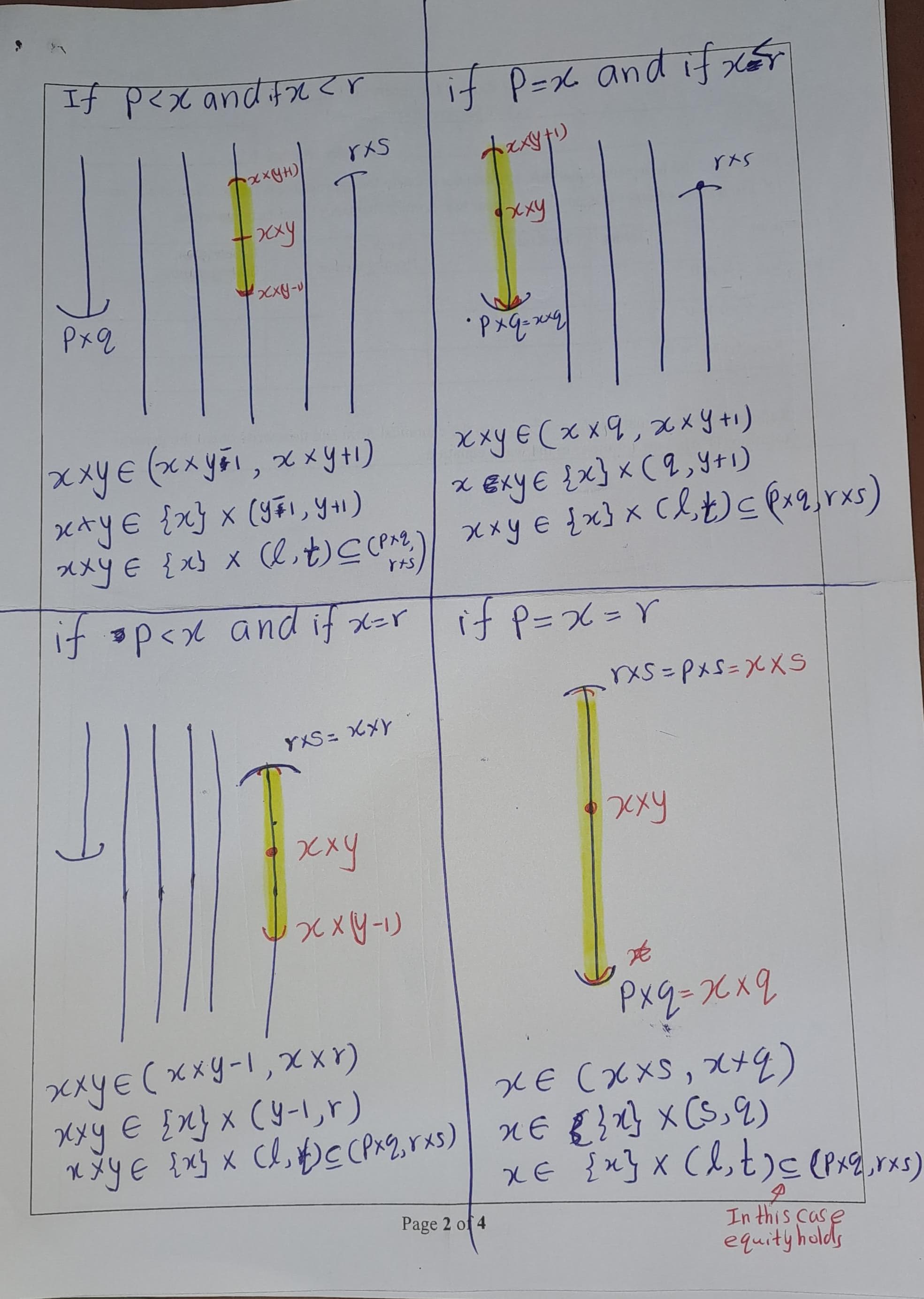
Figure 4.2: $~$

Let $I = [0, 1]$. Compare the product topology on $I \times I$, the dictionary order topology on $I \times I$, and the topology $I \times I$ inherits as a subspace of $\mathbb{R} \times \mathbb{R}$ in the dictionary order topology.

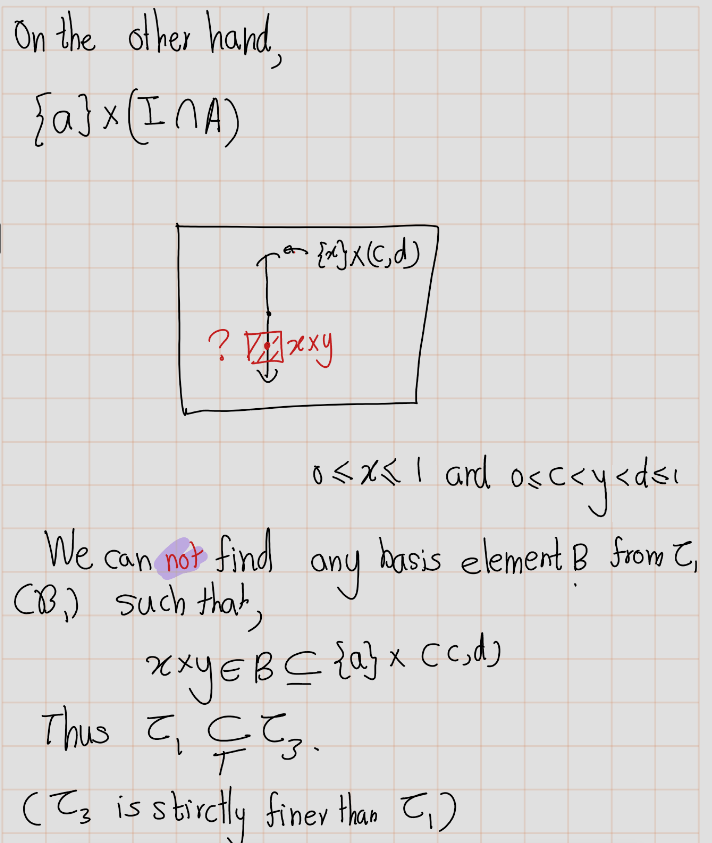
Claim: $\mathcal{T_2}\subsetneq\mathcal{T3}$
So, as previous we have to prove two things they are finer condition and strictly condition.

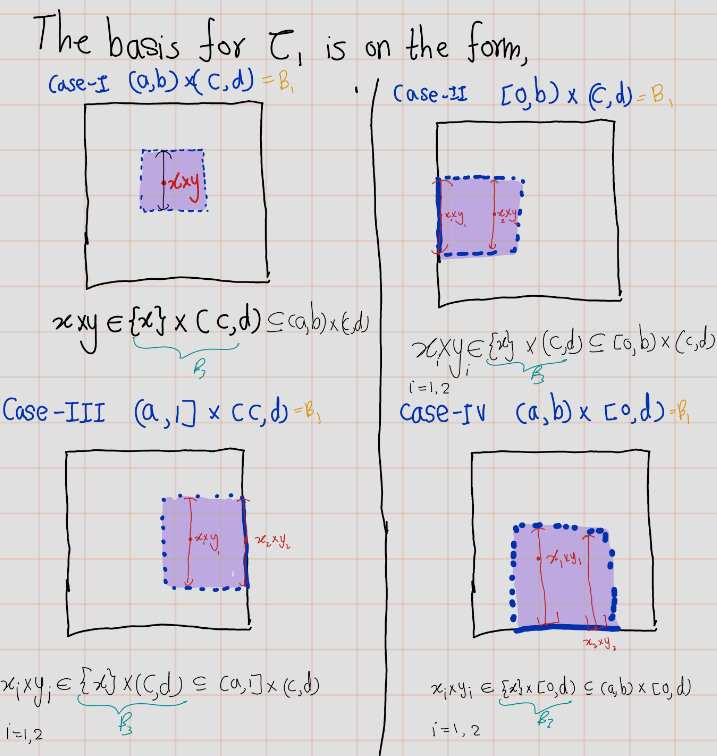
Let $(a_1\times b_1, a_2 \times b_2)$ be a basis element of order topology. and $x\times y \in (a_1\times b_1, a_2 \times b_2)$

Case I $(a_1<x<a_2)$: \[x\times y \in (x\times-1,x\times 2)\cap I^2= [x\times 0,x\times 1]=\{x\}\times [0,1] \subset (a_1\times b_1, a_2 \times b_2)\] Note that $(x\times -1,x\times 2)\cap I^2$ is a basis element of subspace topology.
Case II $(a_1=x<a_2)$: \[x\times y \in (x\times b_1,x\times 2)\cap I^2= [x\times b_1,x\times 1]=\{x\}\times (b_1,1] \subset (a_1\times b_1, a_2 \times b_2)\] Note that $(x\times b_1,x\times 2)\cap I^2$ is a basis element of subspace topology.
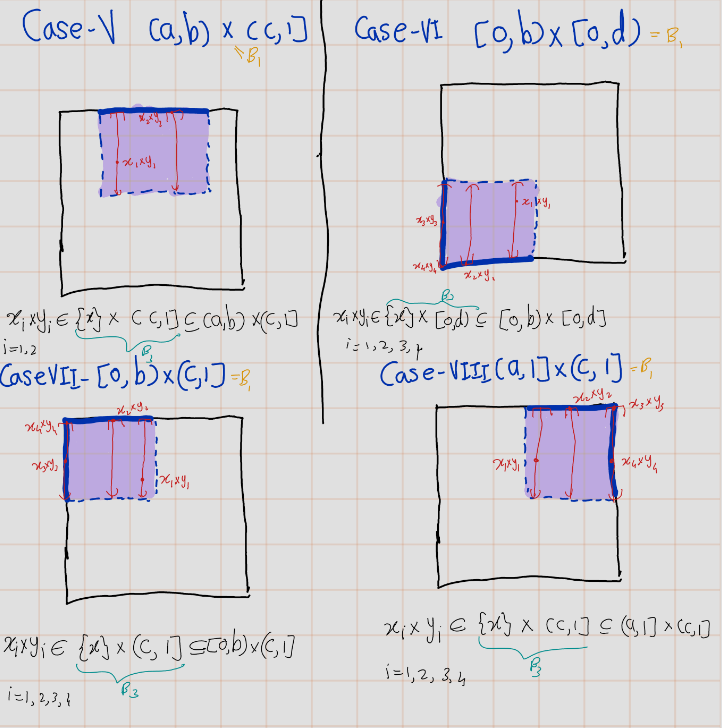
Case III $(a_1<x=a_2)$: \[x\times y \in (x\times -1,x\times b_2)\cap I^2= [x\times 0,x\times b_2]=\{x\}\times [0,b_2) \subset (a_1\times b_1, a_2 \times b_2)\] Note that $(x\times -1,x\times b_2)\cap I^2$ is a basis element of subspace topology.
Case IV $(a_1=x=a_2)$: \[x\times y \in (x\times b_1,x\times b_2)\cap I^2= [x\times b_1,x\times b_2]=\{x\}\times [b_1,b_2) \subset (a_1\times b_1, a_2 \times b_2)\] Note that $(x\times b_1,x\times b_2)\cap I^2$ is a basis element of subspace topology.

See figure 4.3

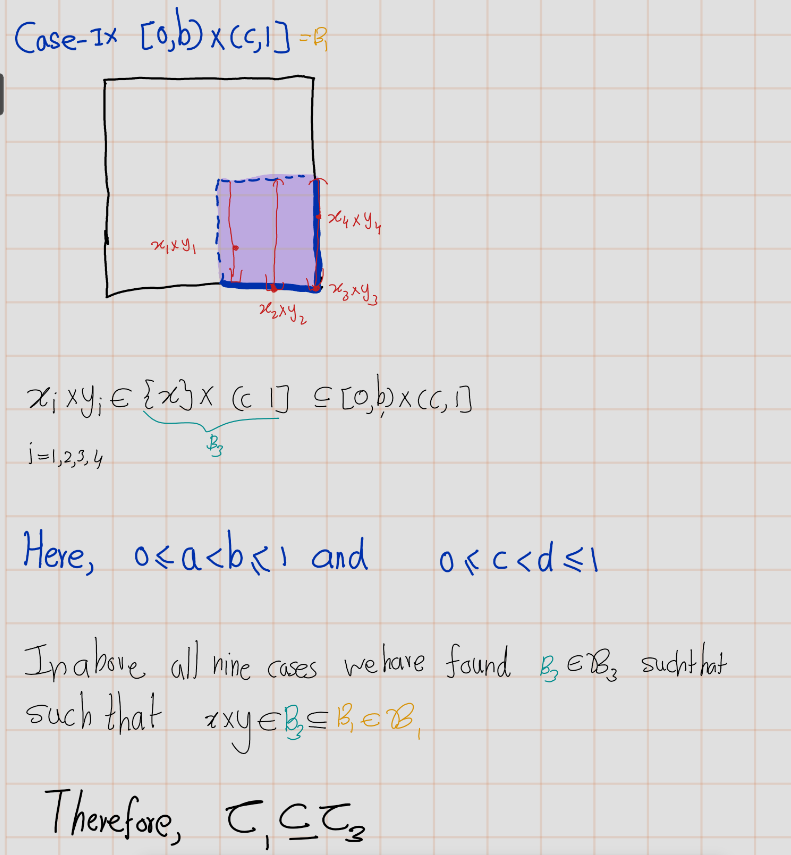
In above all four cases, we have found basis element of subspace topology that contain $x\times y$ and contained in $(a_1\times b_1, a_2 \times b_2)$. Therefore, $\mathcal{T_2}\subsetneq\mathcal{T3}$

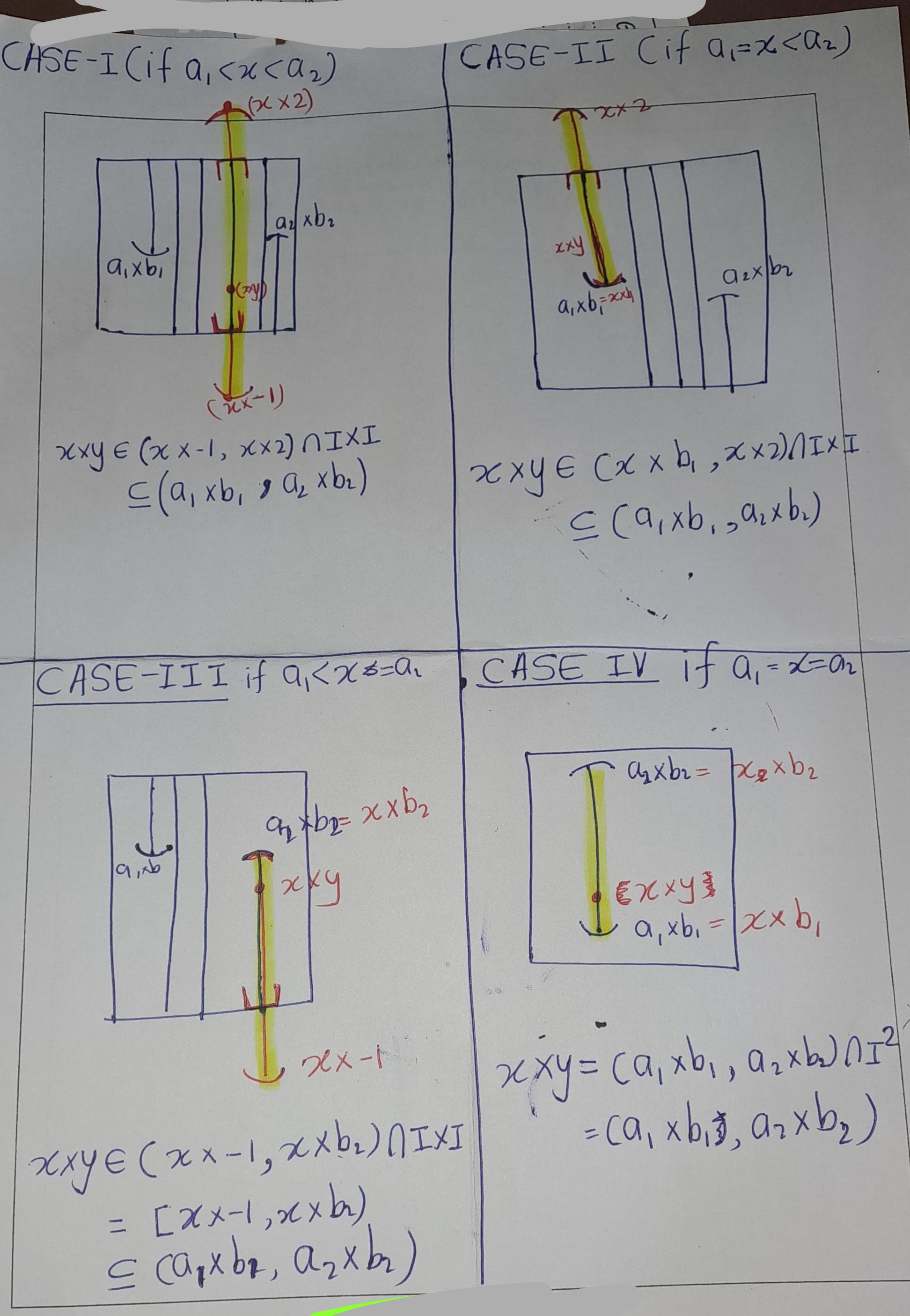
Figure 4.3: $~$

4.3 Section 17 in Munkress Book

Exercise 4.18 (Mun 2.17.1) Let $\mathcal{C}$ be a collection of subsets of the set $X$. Suppose that $$and $X$ are in $\mathcal{C}$, and that finite unions and arbitrary intersections of elements of $\mathcal{C}$ are in $\mathcal{C}$. Show that the collection \[\mathcal{T} = \{X \setminus C | C\in \mathcal{C}\}\] is a topology on X.

Solution:

Proof.

(T1)
- $\emptyset \in \mathcal{C}\implies X\setminus \emptyset=X \in \mathcal{T}$.
- $X \in \mathcal{C}\implies X\setminus X=\emptyset \in \mathcal{T}$
(T2) Let $\{U_\alpha\}_{\alpha\in J}$ be family of elements in $\mathcal{C}$. Then $(X\setminus U_\alpha\}_{\alpha\in J}\in \mathcal{T}$. Then, \[\bigcup_{\alpha\in J}(X\setminus U_\alpha)=X\setminus \bigcup_{\alpha\in J}U_\alpha\] Since $\mathcal{C}$ is closed arbitrary intersection, $\bigcup_{\alpha\in J}\in \mathcal{C}$. Thus,$\bigcap_{\alpha\in J}(X\setminus U_\alpha)=X\setminus \bigcup_{\alpha\in J}U_\alpha\in \mathcal{T}$.
(T3) Let $U_1,U_2,...,U_n\in \mathcal{C}$. Then $(X\setminus U_1),(X\setminus U_2),...,(X\setminus U_n)\in \mathcal{T}$. Then, \[\bigcap_{i=1}^n(X\setminus U_i)=X\setminus \bigcup_{i=1}^nU_i\] Since $\mathcal{C}$ is closed under finite union, $\bigcup_{i=1}^nU_i\in \mathcal{C}$. Thus,$\bigcap_{i=1}^n(X\setminus U_i)=X\setminus \bigcup_{i=1}^nU_i\in \mathcal{T}$. Therefore $\mathcal{T}$ is a topology on $X$.

Exercise 4.19 (Mun 2.17.2) Show that if $A$ is closed in $Y$ and $Y$ is closed in $X$, then $A$ is closed in $X$.

Proof. Since $Y$ is subspace in $X$ and $A$ is closed in $Y$, by theorm 1.3, then there exist closed set $C$ in $X$ such that \[A=Y\cap C\] Since, $Y$ is closed in $X$ and $X$ is toplogical space, $A=Y\cap C$ is closed in $X$.

Exercise 4.20 (Mun 2.17.3) Show that if $A$ is closed in $X$ and $B$ is closed in $Y$ , then $A\times B$ is closed in $X\times Y$

Proof. Suppose that $A$ is closed in $X$ and $B$ is closed in $Y$. Then $X\setminus A$ is open in $X$ and $X\setminus B$ is open in $Y$.

Claim: $(X\times Y) \setminus (A\times B)= ((X\setminus A)\times Y)\cup((X\times (Y\setminus B)))$
Proof of Claim: \[\begin{eqnarray} (x\times y)\in (X\times Y) \setminus (A\times B) &\iff & (x\times y)\not\in (A\times B)\\ &\iff & x\not\in A \text{ or } y \not\in B\\ &\iff & x\in X\setminus A \text{ or } y \in Y\setminus B\\ &\iff& (x\times y) \in ((X\setminus A)\times Y)\cup((X\times (Y\setminus B))) \end{eqnarray}\] So, now we are done proof of the claim. Thus, $(X\times Y) \setminus (A\times B)$ is union of open sets and hence, $(X\times Y) \setminus (A\times B)$ is open in $X \times Y$. Thus, $(A\times B)$ is closed in $X\times Y$.

Exercise 4.21 (Mun 2.17.4) Show that if $U$ is open in $X$ and $A$ is closed in $X$, then $U \setminus A$ is open in $X$, and $A \setminus U$ is closed in $X$.

Proof. Suppose that $U$ is open in $X$ and $A$ is closed in $X$.

Claim 1: $(U\setminus A)=U\cap (X\setminus A)$.
\[\begin{eqnarray} x \in (U\setminus A) &\iff& x\in U \text{ and } x\not\in A\\ &\iff& x\in U \text{ and } x\in X\setminus A\\ &\iff& x\in U \cap X\setminus A\\ \end{eqnarray}\] Since, $A$ is closed in $X$, $X\setminus A$ is open in $X$. Thus, $(U\setminus A)=U\cap (X\setminus A)$ is open in $X$. (By finite intersection property.)

Claim 2: $(A\setminus U)=A\cap (X\setminus U)$.
Similar to proof of claim 1 we can prove this claim.

Since, $U$ is open in $X$, $X\setminus U$ is closed in $X$. Thus, $(A\setminus U)=A\cap (X\setminus U)$ is closed in $X$.

Exercise 4.22 (Mun 2.17.5) Let $X$ be an ordered set in the order topology. Show that $\overline{(a, b)} \subseteq [a, b]$. Under what conditions does equality hold?

Proof. (Proof of $\overline{(a, b)} \subseteq [a, b]$)

Claim 1: $[a,b]$ is closed in $X$ under order toplology.
Observe that, \[X\setminus[a,b] =(-\infty,a)\cup (b,\infty).\] Note that, $(-\infty,a)$ and $(b,\infty)$ are open rays. Then $(-\infty,a)\cup (b,\infty)=X\setminus [a,b]$ is open. Thus, $[a,b]$ is closed in $X$ under order toplogy.

Claim 2: $(a,b)\subseteq [a,b]$
Now, let $x \in (a, b)$ then $a < x < b$ so clearly $a \leq x \leq b$ so $x$ is in $[a, b]$. Thus $(a,b)\subseteq [a,b]$.

Therefore, by cliam 1 and 2, $[a, b]$ is a closed set containing $(a, b)$.

Now, to show $\overline{(a, b)} \subseteq [a, b]$, recall that $\overline{(a, b)}$ is the intersection of all closed sets containing $(a, b)$. Let $x \in \overline{(a, b)}$ Since, $x$ is in every closed set containing $(a, b)$ and $[a, b]$ is a closed set containing $(a, b)$,then $x \in [a, b]$ as needed.

Let $a^{+} = \inf\{x : x > a\}$ and let $b^{-} = \sup\{x : x < b\}$. Consider the closed set $[x, y]$. If $[x, y]$ contains $(a, b)$, then $x \leq a^{+}$ and $y \geq b^{-}$. Thus there exists a closed set containing $(a, b)$ that does not contain $a$ or $b$ if and only if $a^{+} \neq a$ or $b^{-} \neq b$. This is true exactly when $a$ has an immediate successor or $b$ has an immediate predecessor.

For example, in the order topology on $\mathbb{Z}$, \[\overline{(1, 4)} = [2, 3] \subsetneq [1, 4].\]

Exercise 4.23 (Mun 2.17.6) Let $A$, $B$, and $A_{\alpha}$ denote subsets of a space $X$. Prove the following:

If $A \subset B$, then $\overline{A} \subset \overline{B}$.
$\overline{A \cup B} = \overline{\overline{A}} \cup \overline{\overline{B}}$.
$\overline{\bigcup A_{\alpha}} \supseteq \bigcup \overline{A_{\alpha}}$; give an example where equality fails.

Proof. Let $A$, $B$, and $A_{\alpha}$ denote subsets of a space $X$.

By definition, $\overline{A}$ is the intersection of all closed sets containing $A$. Since $\overline{B}$ is a closed set that contains $B$ and hence $A$, it must therefore contain $\overline{A}$.

Claim 1: $\overline{A \cup B} \supseteq {\overline{A}} \cup {\overline{B}}$
The set $\overline{A \cup B}$ is a closed set that contains $A \cup B$, so it contains both $A$ and $B$, and therefore it contains both $\overline{A}$ and $\overline{B}$. Therefore, $\overline{A \cup B} \supseteq {\overline{A}} \cup {\overline{B}}$.
Claim 2: $\overline{A \cup B} \subseteq {\overline{A}} \cup {\overline{B}}$
${\overline{A}} \cup \overline{B}$ is a closed set (since it is the union of two closed sets) that contains $A \cup B$, (Beacuse $A\subseteq\overline{A}$ and $B \subseteq \overline{B}\implies A \cup B \subseteq \overline{A} \cup \overline{B}$.) so it contains $\overline{A \cup B}$.

The set $\overline{\bigcup A_{\alpha}}$ is a closed set that contains each $A_{\alpha}$, so it contains each $\overline{A_{\alpha}}$, and thus it contains $\bigcup \overline{A_{\alpha}}$. Thus, $\overline{\bigcup A_{\alpha}} \supseteq \bigcup \overline{A_{\alpha}}$
(But we can’t do the converse because an arbitrary union of closures isn’t necessarily closed!)

Example 1 that equality fails,
Let $A_n$ be the closed set $[\frac{1}{n}, 1] \subset \mathbb{R}$. Then \[\bigcup_{n \in \mathbb{N}} \overline{A_n} = \bigcup_{n \in \mathbb{N}} A_n =\bigcup_{n \in \mathbb{N}} [\frac{1}{n}, 1] = (0, 1], \text{ But } \bigcup_{n \in \mathbb{N}} A_n = [0, 1]\].
Example 2 that equality fails,
Consider $\mathbb{R}$ with the standard topology and all one-point sets $\{q\}$ with $q$ rational. Then $\overline{\{q\}} = \{q\}$ for every such set, so that $\bigcup_{q \in \mathbb{Q}} \overline{\{q\}} = \mathbb{Q}$, but $\overline{\bigcup_{q \in \mathbb{Q}} \{q\}} = \overline{\mathbb{Q}} = \mathbb{R}$.

Exercise 4.24 (Mun 2.17.7) Criticize the following “proof” that $\overline{\cup A_\alpha} \subset \cup \overline{A_\alpha}$:
if $\{A_\alpha\}$ is a collection of sets in $X$ and if $x \in \overline{\cup A_\alpha}$, then every neighborhood $U$ of $x$ intersects $\cup A_\alpha$.Thus $U$ must intersect some $A_\alpha$, so that $x$ must belong to the closure of some $A_\alpha$. Therefore, $x \in \cup \overline{A_\alpha}$.

Solution: If $\{A_\alpha\}$ is a collection of sets in $X$ and if $x \in \overline{\cup A_\alpha}$, then every neighborhood $U$ of $x$ intersects $\cup A_\alpha$.Thus $U$ must intersect some $A_\alpha$. But this $A_{\alpha}$ may be distinct for different neighbourhoods, so not necessarily every neighbourhood $U$ of $A_{\alpha}$ intersects the same $A_{\alpha}$. Hence we cannot conclude that $x$ must belong to the closure of some fixed $A_{\alpha}$.

Exercise 4.25 (Mun2.17.8) Let $A$, $B$, and $A_{\alpha}$ denote subsets of a space $X$. Determine whether the following equations hold; if an equality fails, determine whether one of the inclusions $\supset$ or $\subset$ holds. (a) $A \cap B = \overline{A} \cap \overline{B}$. (b) $\bigcup A_{\alpha} = \bigcup \overline{A_{\alpha}}$. (c) $A - B = \overline{A} - B$.

Solution

(a)

(b)

(c)

Exercise 4.26 (Mun 2.17.9) Let $A \subset X$ and $B \subset Y$. Show that in the space $X \times Y$, \[\overline{A \times B} = \overline{A} \times \overline{B}\].

Exercise 4.27 (Mun 2.17.10) Show that every order topology is Hausdorff.

Exercise 4.28 (Mun 2.17.11) Show that the product of two Hausdorff spaces is Hausdorff.

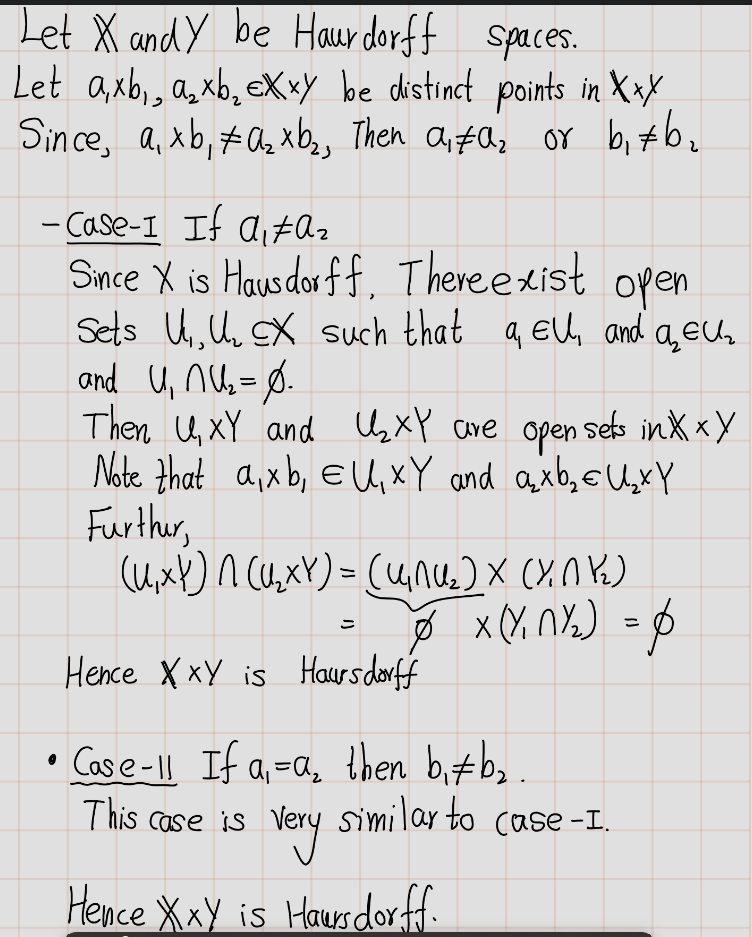
Exercise 4.29 (Mun 2.17.12) Show that a subspace of a Hausdorff space is Hausdorff.

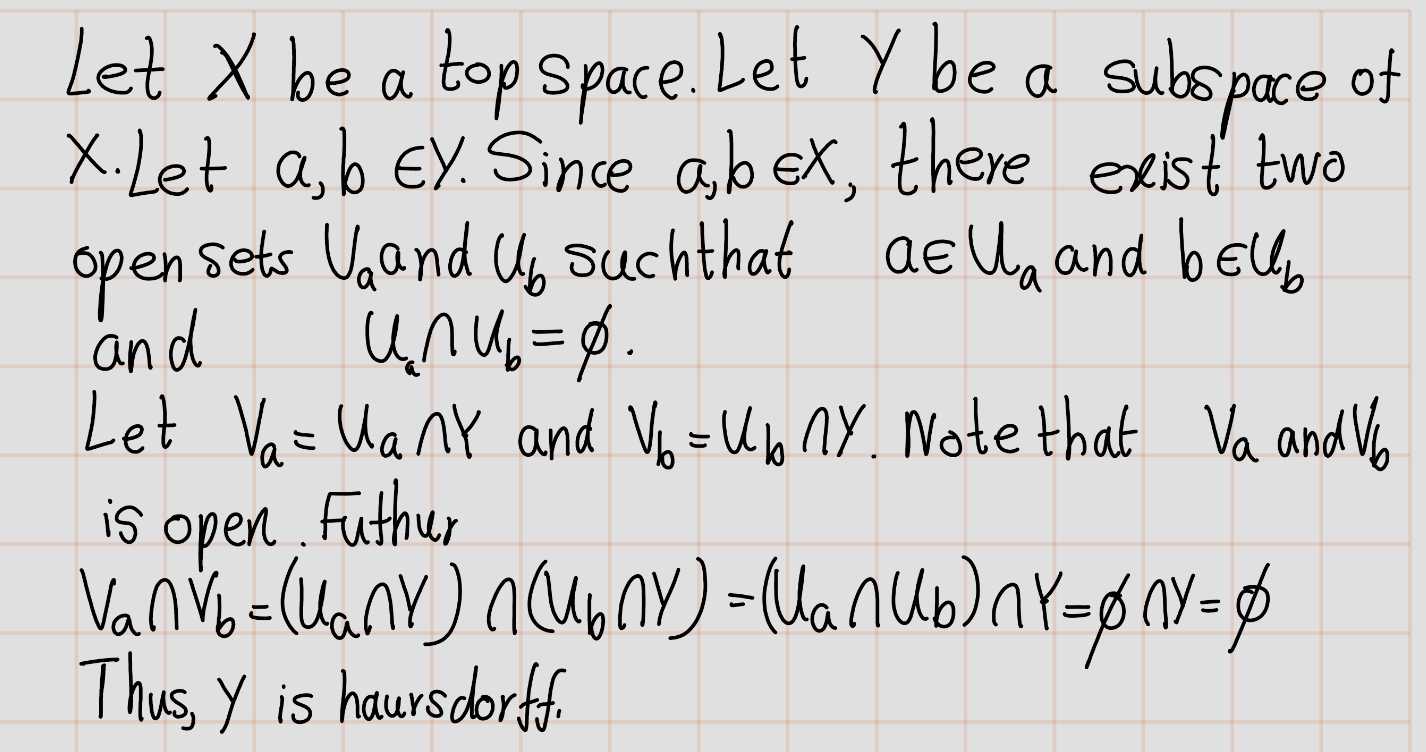
Exercise 4.30 (Mun 2.17.13) Show that $X$ is Hausdorff if and only if the diagonal $\Delta = \{x\times x | x \in X\}$ is closed in $X \times X$.

Exercise 4.31 (Mun 2.17.14) In the finite complement topology on $\mathbb{R}$, to what point or points does the sequence $x_n = \frac{1}{n}$ converge?

Exercise 4.32 (Mun 2.17.15) Show the $T_1$ axiom is equivalent to the condition that for each pair of points of $X$, each has a neighborhood not containing the other.

Exercise 4.33 Consider the following five topologies on $\mathbb{R}$ given

\[\begin{eqnarray} \mathcal{T_1} &:=& \text{the standard topology},\\ \mathcal{T_2} &:=& \text{the topology of } \mathbb{R}_K ,\\ \mathcal{T_3} &:=& \text{the finite complement topology,}\\ \mathcal{T_4} &:=& \text{the upper limit topology, having all sets $(a, b]$ as basis},\\ \mathcal{T_5} &:=& \text{the topology having all sets $(-\infty, a) = \{x | x < a\}$ as basis.}\\ \end{eqnarray}\]

Determine the closure of the set $K = \left\{1/n | n \in \mathbb{Z}^+\right\}$ under each of these topologies.
Which of these topologies satisfy the Hausdorff axiom? the $T_1$ axiom?

As a summary

Topologies	$\overline{K}$	Is $T_2$ space ?	Is $T_1$ Space
$\mathcal{T_1}$	$K\cup\{0\}$	$\checkmark$	$\times$
$\mathcal{T_2}$	$K$	$\checkmark$	$\checkmark$
$\mathcal{T_2}$	${0}$	$\checkmark$	$\checkmark$
$\mathcal{T_2}$	$K$	$\checkmark$	$\checkmark$
$\mathcal{T_2}$	$[0,\infty)$	$\checkmark$	$\checkmark$
$\mathcal{T_2}$	${0}$	$\checkmark$	$\checkmark$

Exercise 4.34 (Mun 2.17.17) Consider the lower limit topology on $\mathbb{R}$ and the topology given by the basis $C$ of Exercise 8 of §13. Determine the closures of the intervals $A = (0, \sqrt{2})$ and $B = (\sqrt{2}, 3)$ in these two topologies.

Exercise 4.35 (Mun 2.17.18) Determine the closures of the following subsets of the ordered square: \[\begin{align} A &:= \left\{\frac{1}{n} \times 0 \mid n \in \mathbb{Z}^{+}\right\}, \\ B &:= \left\{\left(1 - \frac{1}{n}\right) \times \frac{1}{2} \mid n \in \mathbb{Z}^{+}\right\}, \\ C &:= \left\{x \times 0 \mid 0 < x < 1\right\}, \\ D &:= \left\{x \times \frac{1}{2} \mid 0 < x < 1\right\}, \\ E &:= \left\{\frac{1}{2} \times y \mid 0 < y < 1\right\}. \end{align}\]

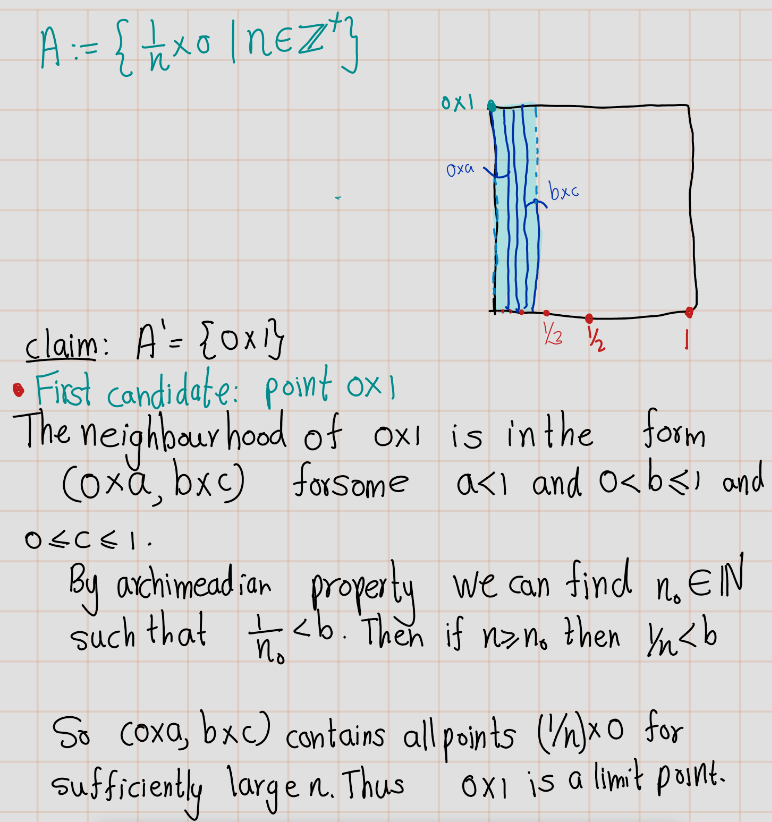
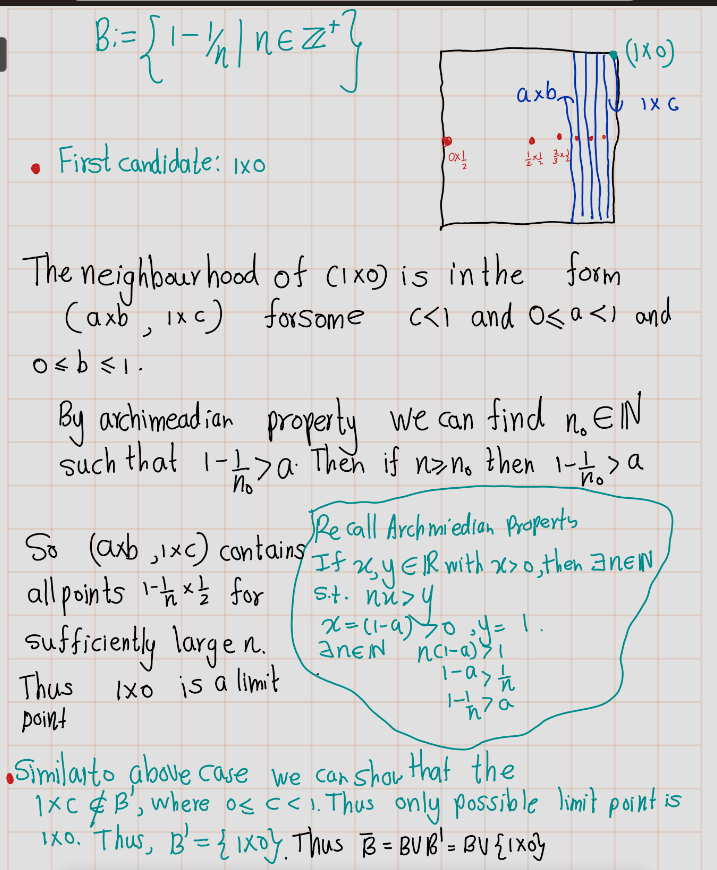
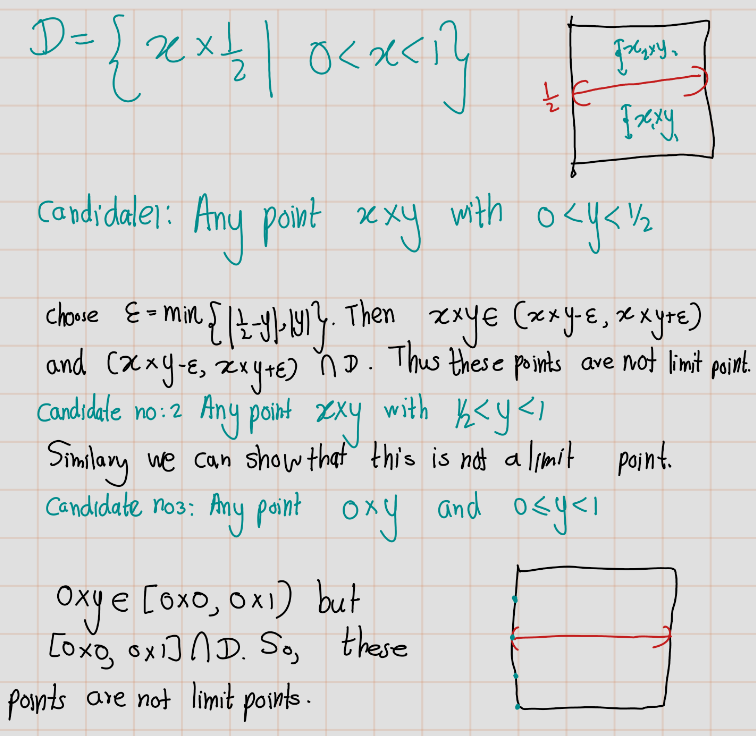
Exercise 4.36 (Mun 2.17.19) If $A \subset X$, we define the boundary of $A$ by the equation \[\text{Bd} \, A = \overline{A} \cap \overline{(X \setminus A)}.\]

Show that $\text{Int} \, A$ and $\text{Bd} \, A$ are disjoint, and $\overline{A} = \text{Int} \, A \cup \text{Bd} \, A$.
Show that $\text{Bd} \, A = \emptyset \Leftrightarrow A$ is both open and closed.
Show that $U$ is open $\Leftrightarrow \text{Bd} \, U = \overline{U} \setminus U$.
If $U$ is open, is it true that $U = \text{Int}(\overline{U})$? Justify your answer.

Solution

Show that $\text{Int} \, A$ and $\text{Bd} \, A$ are disjoint, and $\overline{A} = \text{Int} \, A \cup \text{Bd} \, A$.

Show that $\text{Bd} \, A = \emptyset \Leftrightarrow A$ is both open and closed.

Show that $U$ is open $\Leftrightarrow \text{Bd} \, U = \overline{U} \setminus U$.

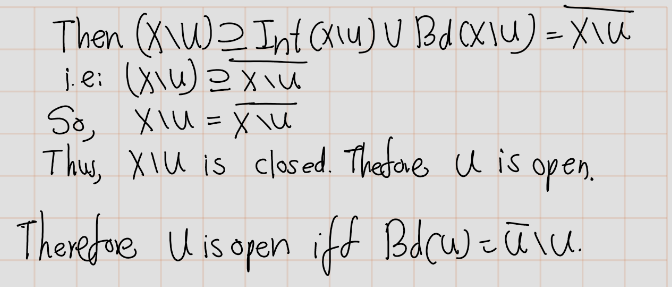
d)(d) If $U$ is open, is it true that $U = \text{Int}(\overline{U})$? Justify your answer.

Exercise 4.37 (Mun 2.17.20) Find the boundary and the interior of each of the following subsets of $\mathbb{R}^2$:

$A = \{(x, y) | y = 0\}$
$B = \{(x, y) | x > 0 \text{ and } y \neq 0\}$
$C = A \cup B$
$D = \{(x, y) | x \text{ is rational}\}$
$E = \{(x, y) | 0 < x^2 - y^2 \leq 1\}$
$F = \{(x, y) | x \neq 0 \text{ and } y \leq \frac{1}{x}\}$

Solution

$A = \{(x, y) | y = 0\}$

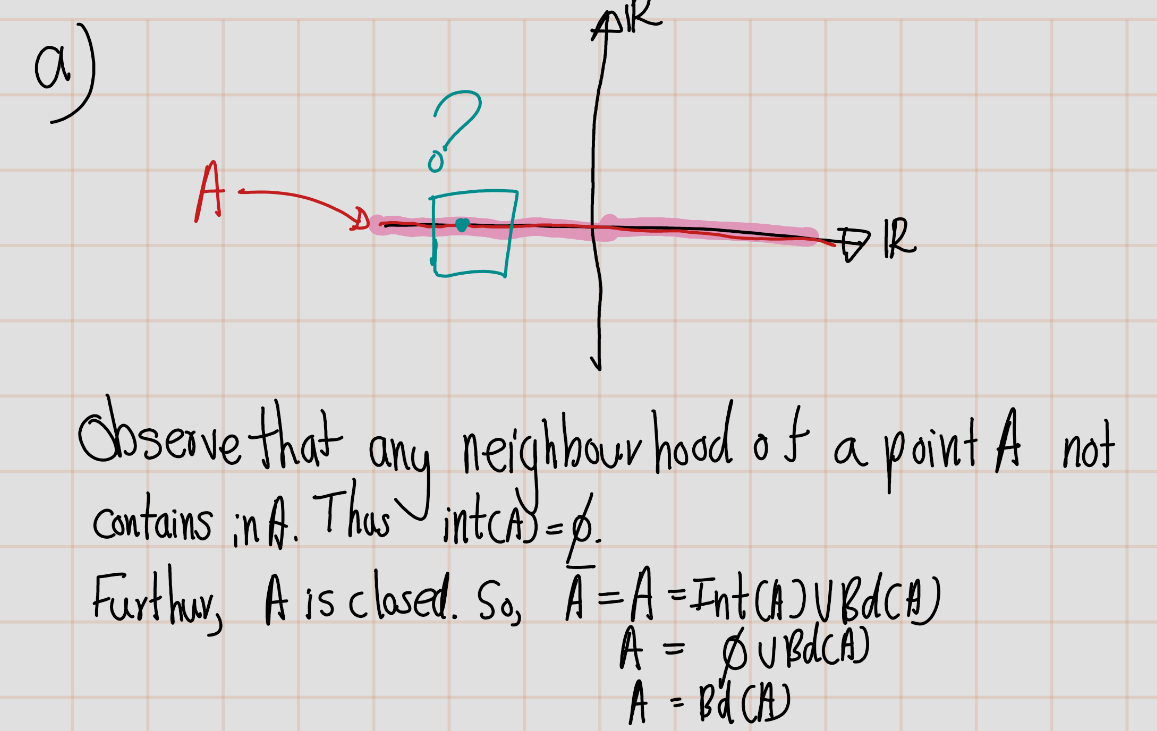
$B = \{(x, y) | x > 0 \text{ and } y \neq 0\}$

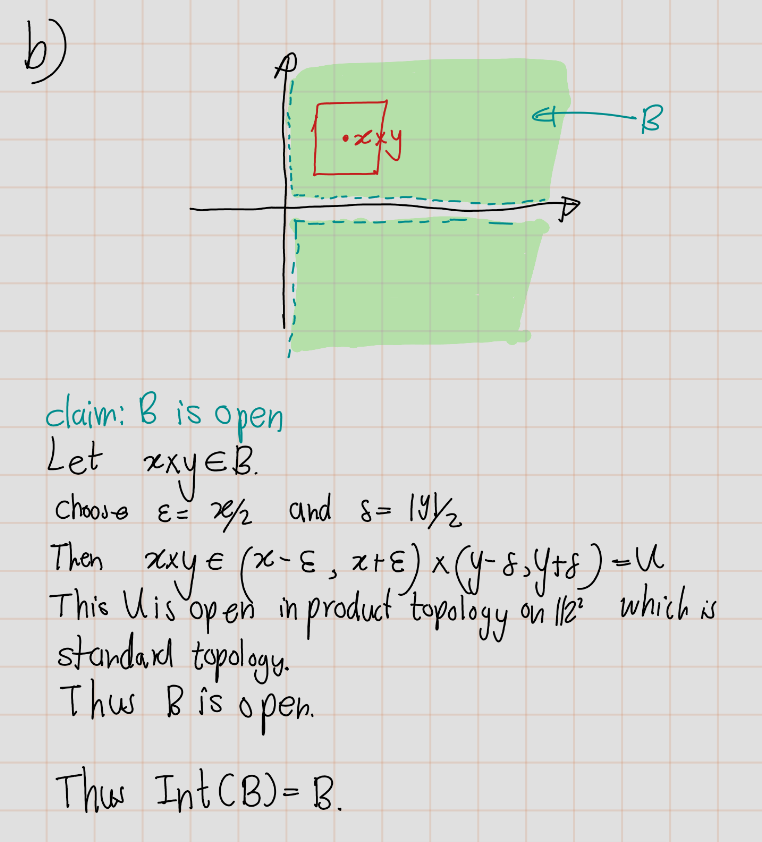
$C = A \cup B$
$D = \{(x, y) | x \text{ is rational}\}$
$E = \{(x, y) | 0 < x^2 - y^2 \leq 1\}$
$F = \{(x, y) | x \neq 0 \text{ and } y \leq \frac{1}{x}\}$

4.4 Section 18 in Munkress Book

Exercise 4.38 (Mun 2.18.1) Proove that the function $f:\mathbb{R}\to\mathbb{R}$, the $\epsilon-\delta$ defintion of continuty implies the open set definition.

Exercise 4.39 (Mun 2.18.2) Suppose that $f:X\to Y$ is continous. If $x$ is a limit point of sub set of $A$ of $X$, is it necessary true that $f(x)$ is a limit point of $f(A)$?

Exercise 4.40 (Mun 2.18.3)

Let $X$ and $X'$ denote a single set in the two topologies $\mathcal{T}$ and $\mathcal{T}'$, respectively. Let $i : X' \rightarrow X$ be the identity function.

Exercise 4.41 (Mun 2.18.4) Given $x_0 \in X$ and $y_0 \in Y$, show that the maps $f : X \rightarrow X \times Y$ and $g : Y \rightarrow X \times Y$ defined by $f(x) = x \times y_0$ and $g(y) = x_0 \times y$ are imbeddings.

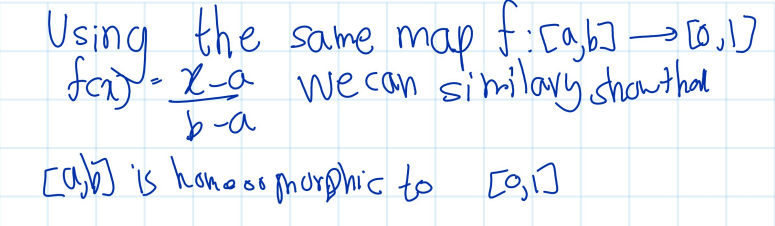
Exercise 4.42 (Mun 2.18.5) Show that the subspace $(a, b)$ of $\mathbb{R}$ is homeomorphic with $(0, 1)$ and the subspace $[a, b]$ of $\mathbb{R}$ is homeomorphic with $[0, 1]$.

Exercise 4.43 (Mun 2.18.6) Find a function $f : \mathbb{R} \to \mathbb{R}$ that is continuous at precisely one point.

Topologies	\(\overline{K}\)	Is \(T_2\) space ?	Is \(T_1\) Space
\(\mathcal{T_1}\)	\(K\cup\{0\}\)	\(\checkmark\)	\(\times\)
\(\mathcal{T_2}\)	\(K\)	\(\checkmark\)	\(\checkmark\)
\(\mathcal{T_2}\)	\({0}\)	\(\checkmark\)	\(\checkmark\)
\(\mathcal{T_2}\)	\(K\)	\(\checkmark\)	\(\checkmark\)
\(\mathcal{T_2}\)	\([0,\infty)\)	\(\checkmark\)	\(\checkmark\)
\(\mathcal{T_2}\)	\({0}\)	\(\checkmark\)	\(\checkmark\)