Chapter 4 Linear Maps Exercises
4.2 Null Space and Injectivity
In this section we will learn about two subspaces that are intimately connected with each linear map. We begin with the set of vectors that get mapped to \(0\).
Definition 4.1 (null space) For \(𝑇\in \mathcal{L}(𝑉,𝑊)\), the null space of \(𝑇\), denoted by \(\text{null}𝑇\), is the subset of \(𝑉\) consisting of those vectors that \(𝑇\) maps to \(0\) (Notation \(\text{null}T\)): \[\text{null} 𝑇 = {𝑣 ∈ 𝑉 ∶ 𝑇𝑣 = 0}\]




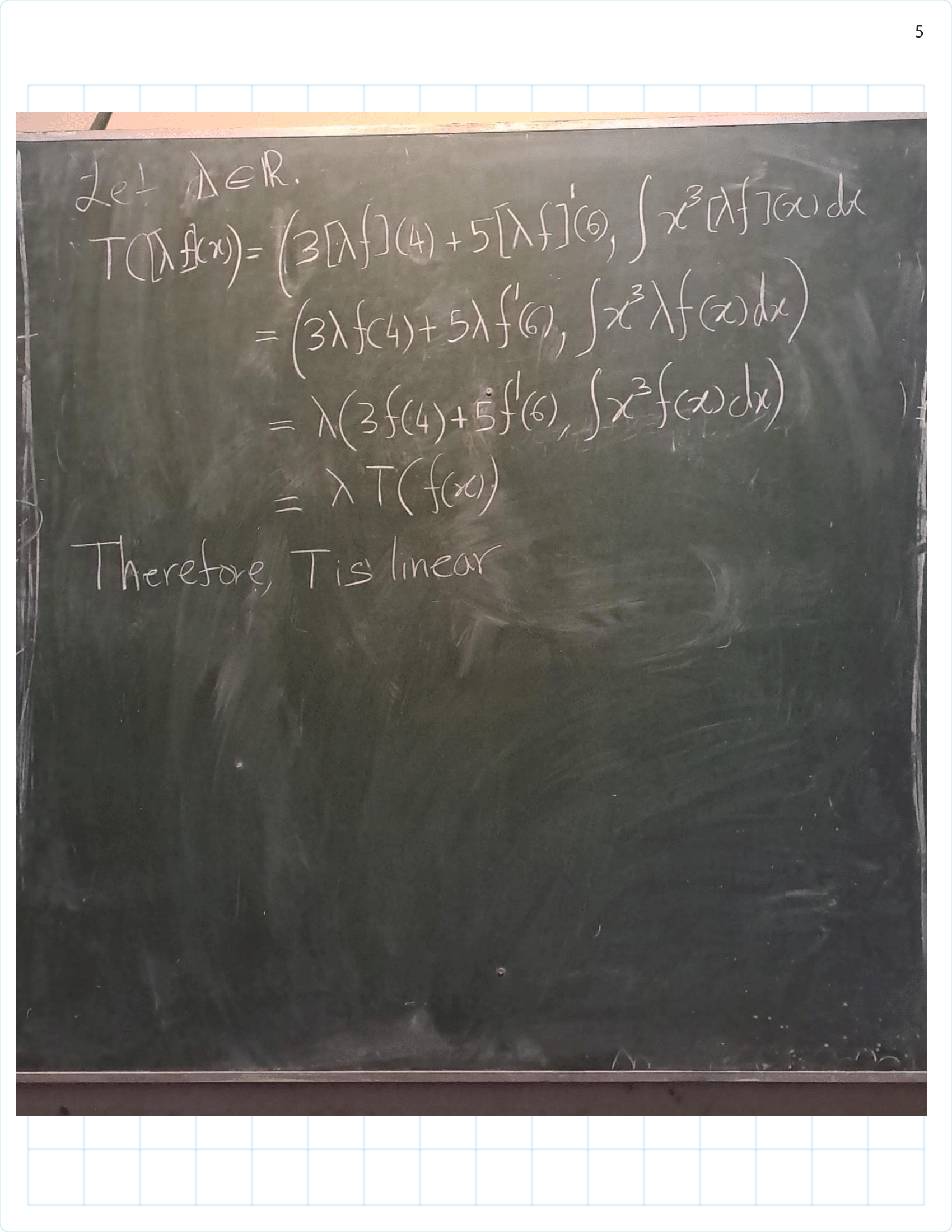
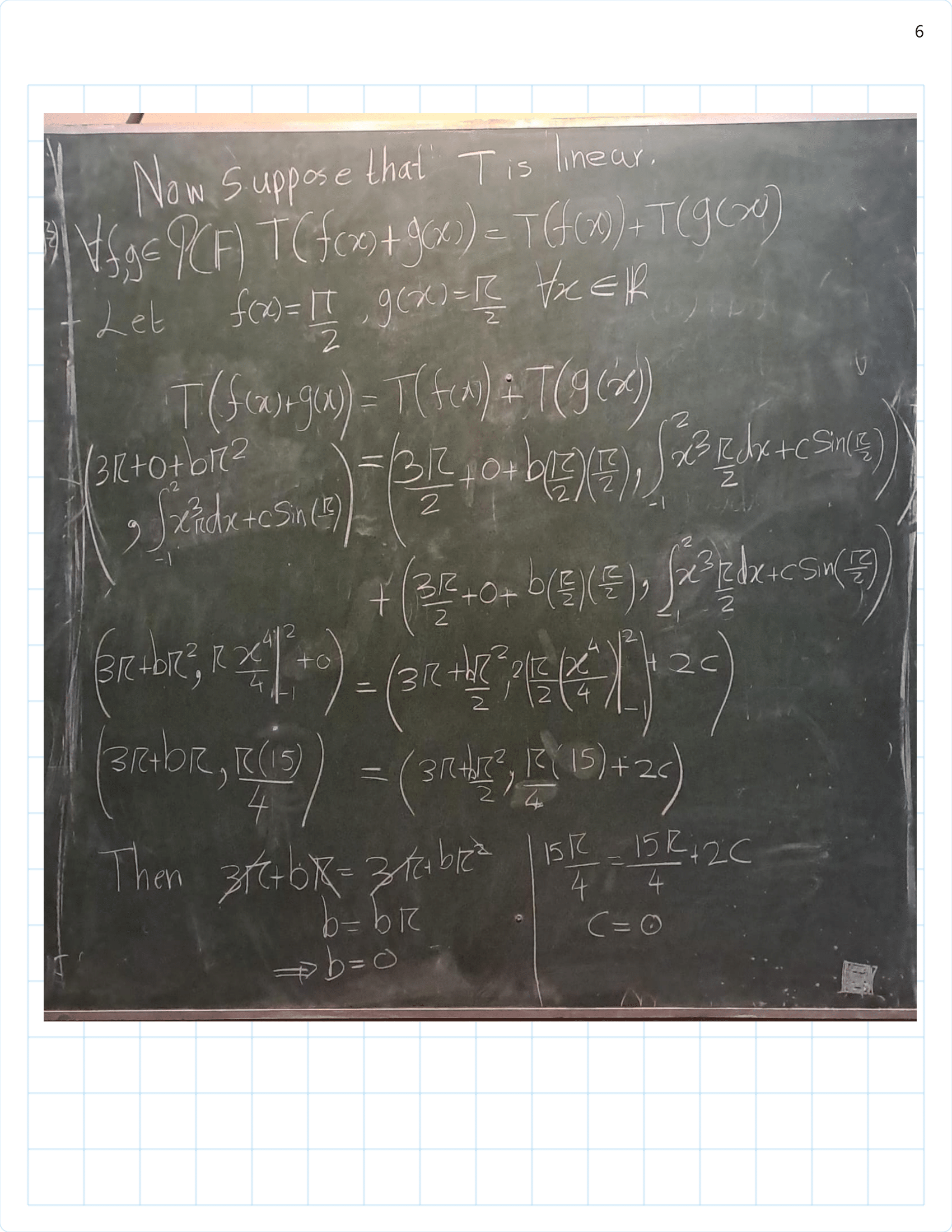




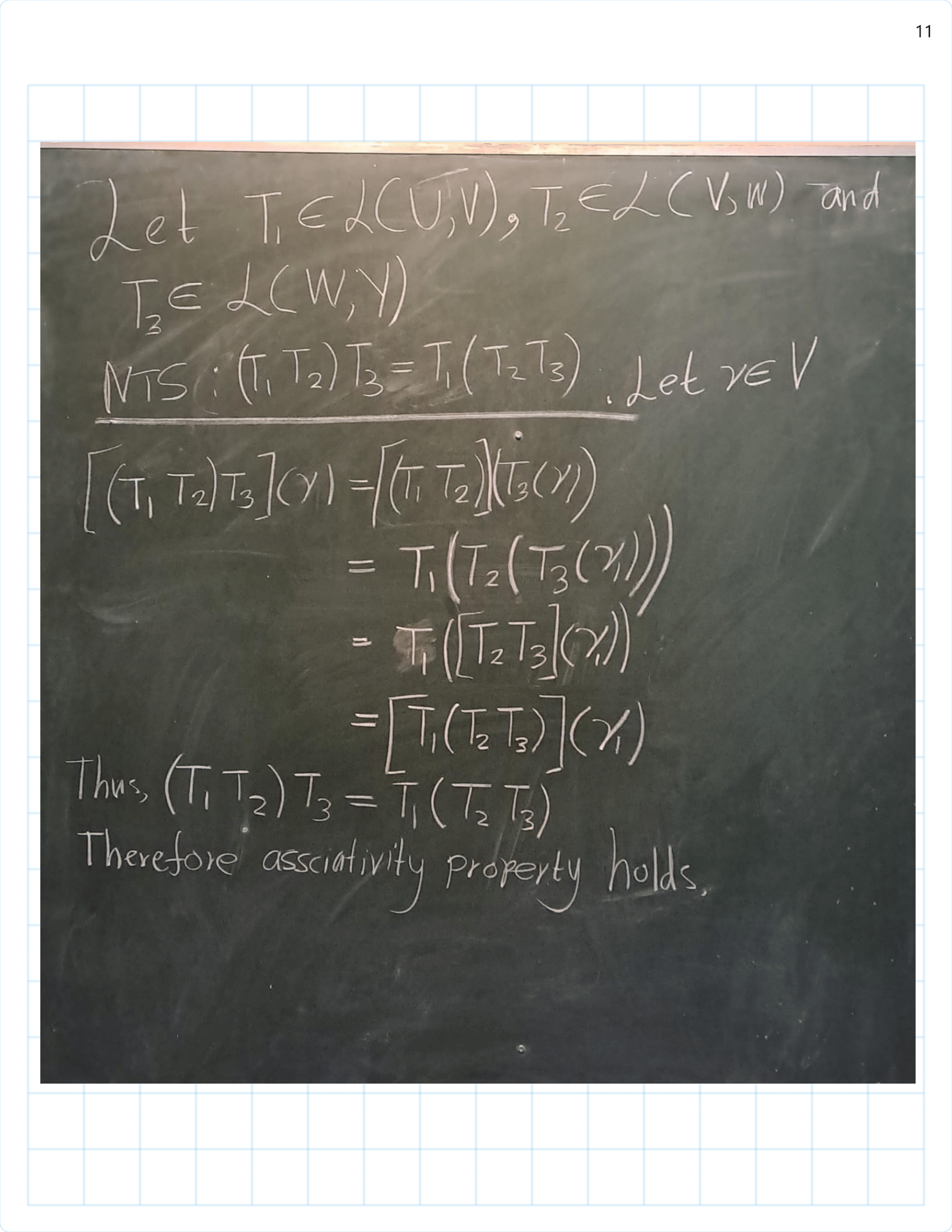
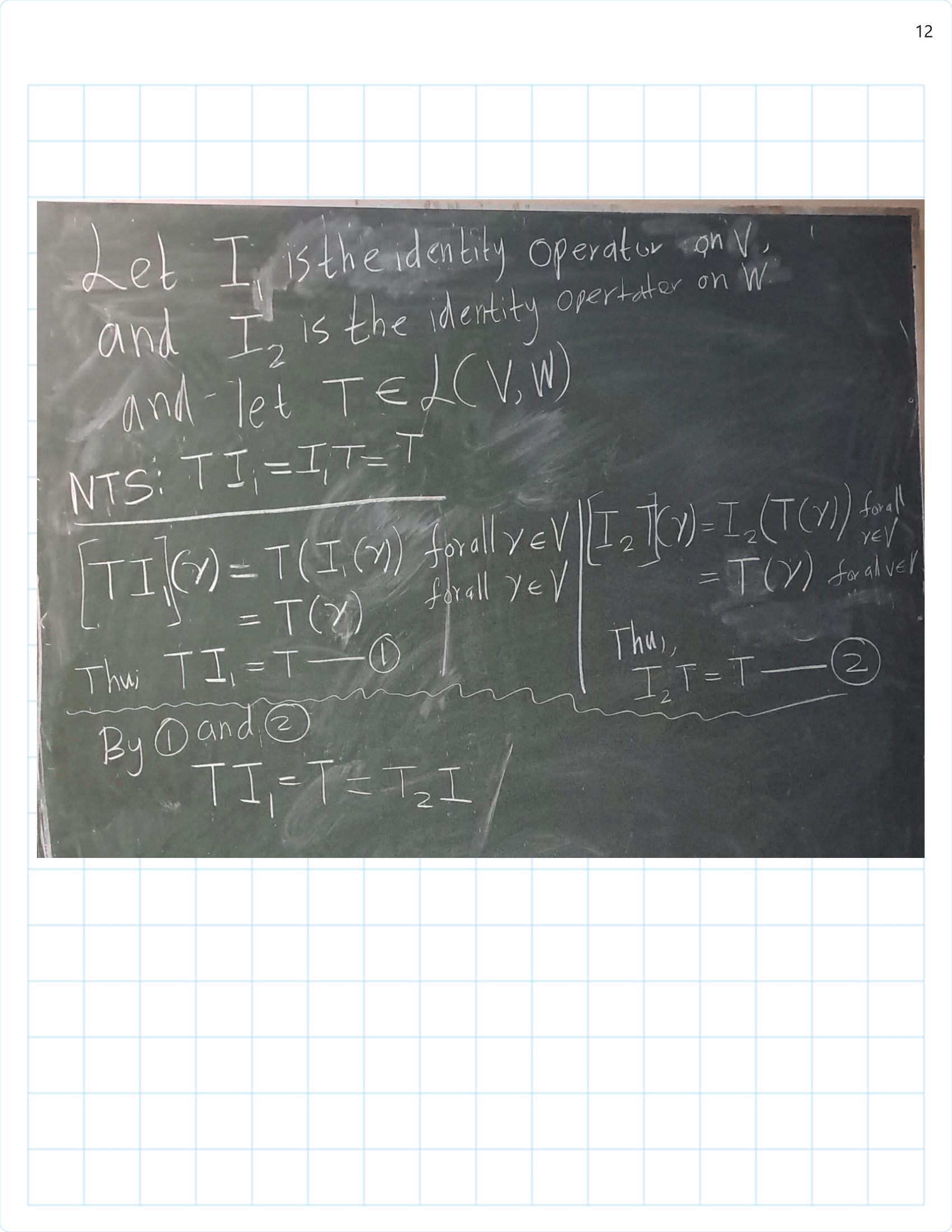

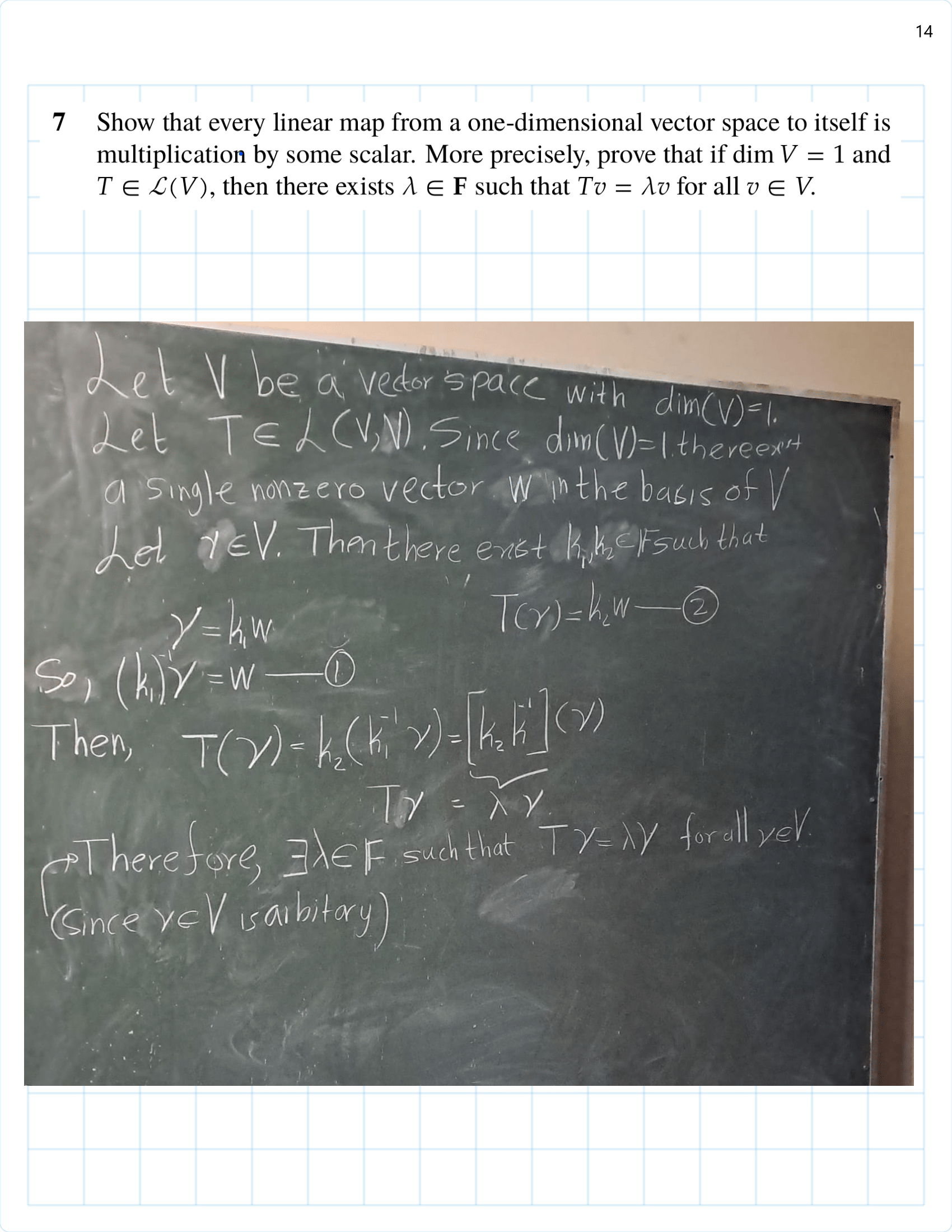




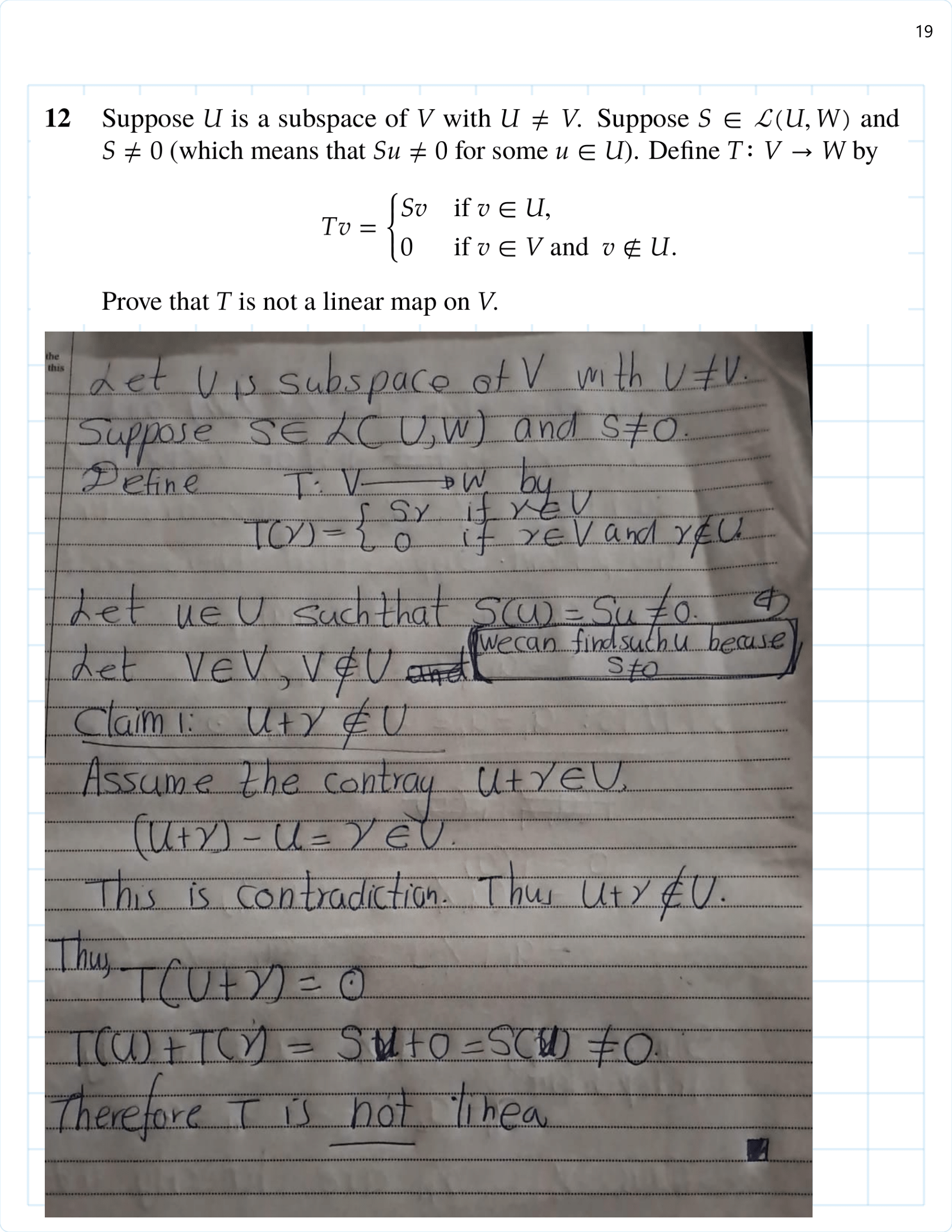


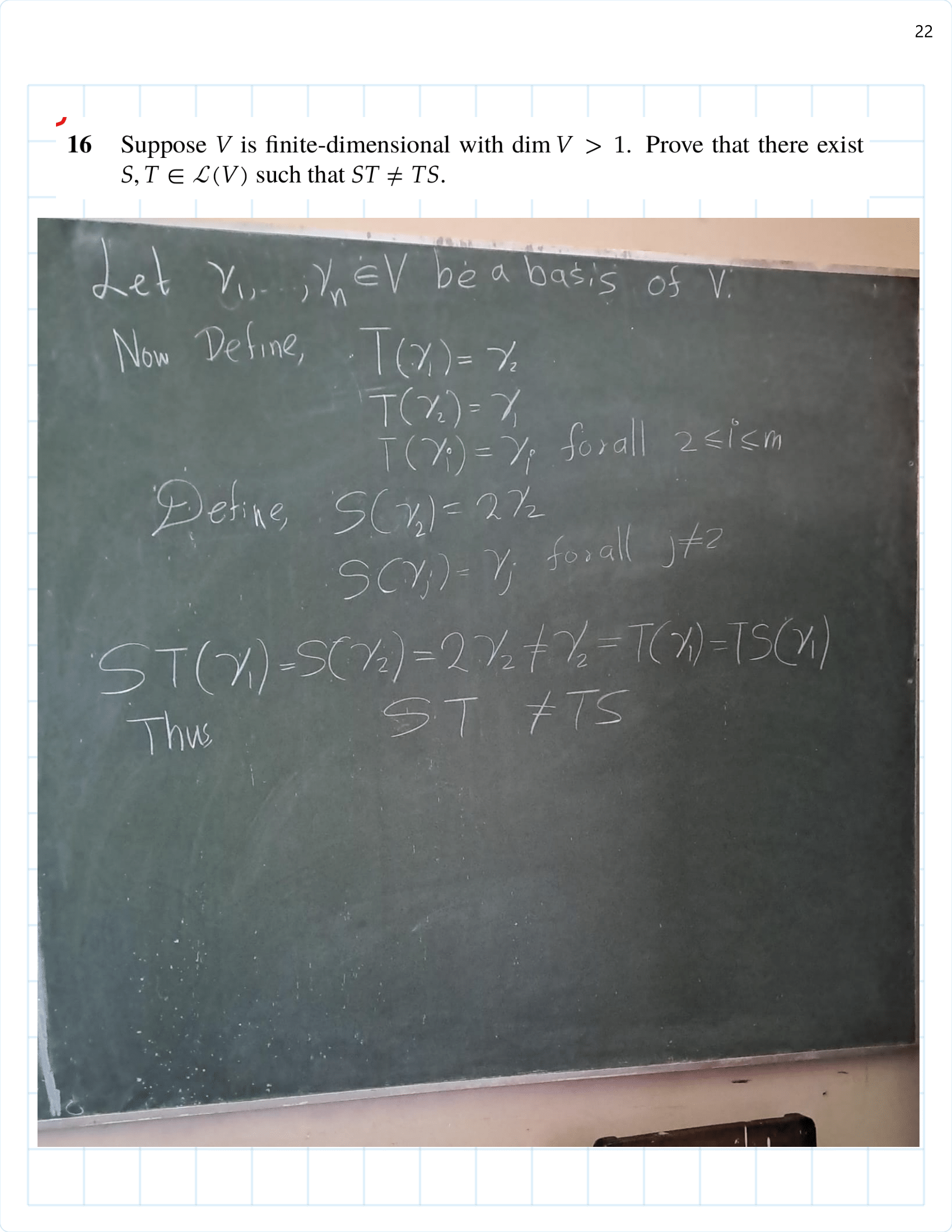

/Exercise%203B%20part(1)-01.png)
/Exercise%203B%20part(1)-02.png)
/Exercise%203B%20part(1)-03.png)
/Exercise%203B%20part(1)-04.png)
/Exercise%203B%20part(1)-05.png)
/Exercise%203B%20part(1)-06.png)
/Exercise%203B%20part(1)-07.png)
/Exercise%203B%20part(1)-08.png)
/Exercise%203B%20part(1)-09.png)
/Exercise%203B%20part(1)-10.png)
/Exercise%203B%20part(1)-11.png)
/Exercise%203B%20part(1)-12.png)
/Exercise%203B%20part(1)-13.png)
/Exercise%203B%20part(1)-14.png)
/Exercise%203B%20part(1)-15.png)
/Exercise%203B%20part(1)-16.png)
/Exercise%203B%20part(1)-17.png)
/Exercise%203B%20part(1)-18.png)
/Exercise%203B%20part(1)-19.png)
/Exercise%203B%20part(1)-20.png)
/Exercise%203B%20part(1)-21.png)
/Exercise%203B%20part(1)-22.png)