Chapter 3 Conformal Mappings

Definition 3.1 (Tanagent Vector) Let \(\gamma(t) = x(t) + iy(t), 0\leq t \leq 1\), be a smooth parameterized curve terminating at \(z_0 = \gamma(0)\). We refer to \[\gamma'(0) = \lim_{t \to 0} \frac{\gamma(t)-\gamma(0)}{t} = x'(0) + iy'(0)\] as the tangent vector to the curve ’Y at ZOo

Definition 3.2 (Angle between two curves ) We define the angle between two curves at \(z_0\) to be the angle between their tangent vectors at \(z_O\).

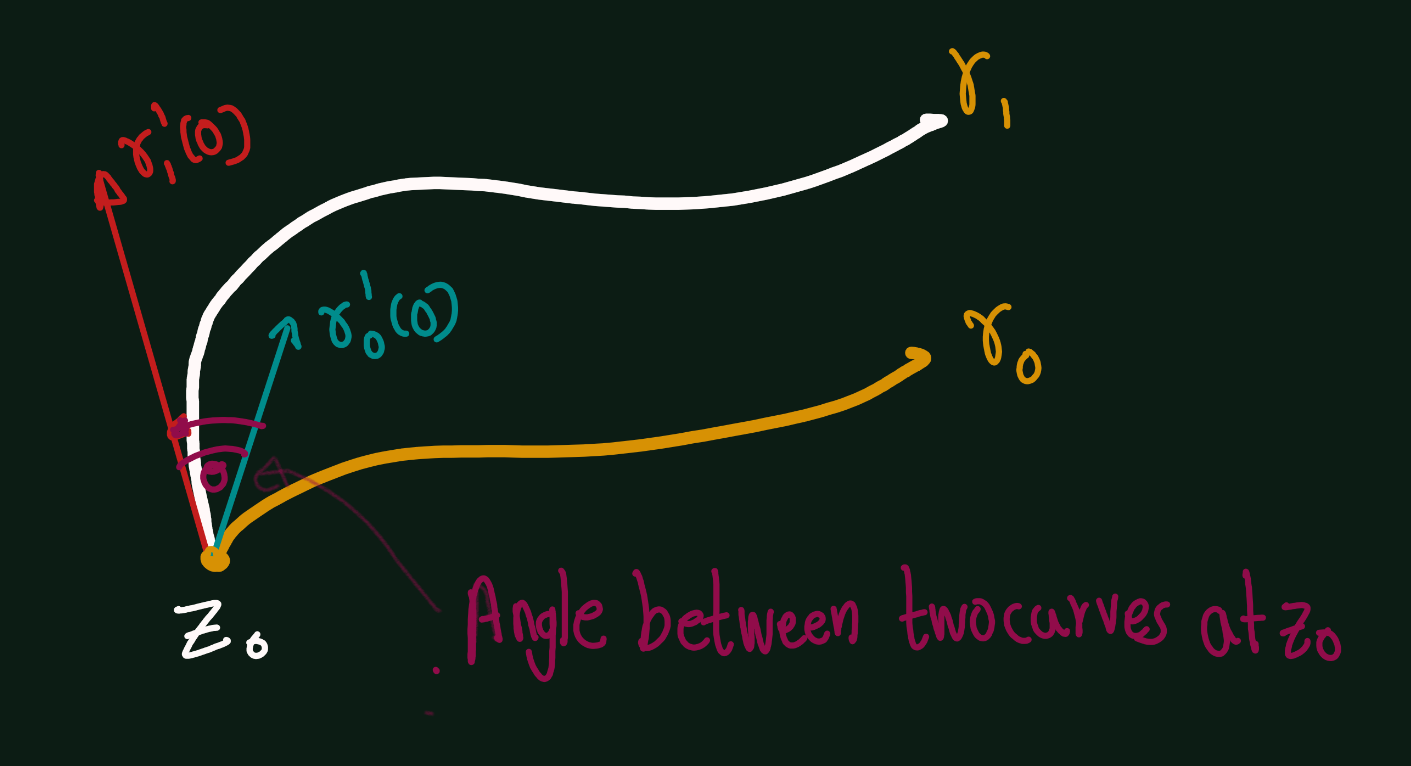
Theorem 3.1 If \(\gamma(t)\), \(0 \leq t \leq 1\), is a smooth parameterized curve terminating at \(z_0 = \gamma(0)\), and \(f(z)\) is analytic at \(z_0\), then the tangent to the curve \(f(\gamma(t))\) terminating at \(f(z_0)\) is given by: \[\begin{equation} (f \circ \gamma)'(0) = f'(z_0)\gamma'(0) \end{equation}\]

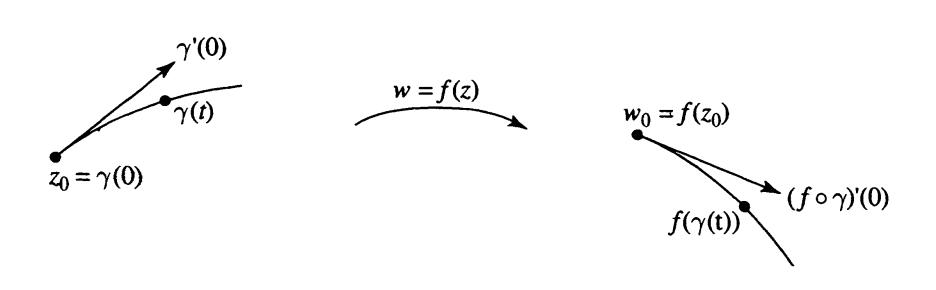
Proof.

• If \(\gamma'(0) \neq 0\), then \(\gamma(t) \neq \gamma(0)\) for \(t\) near \(0\), \(t \neq 0\), so we may write \[\begin{equation} \frac{f(\gamma(t)) - f(\gamma(0))}{t} = \frac{f(\gamma(t)) - f(\gamma(0))}{\gamma(t) - \gamma(0)} \cdot \frac{\gamma(t) - \gamma(0)}{t} \end{equation}\] and pass to the limit, to obtain the formula (6.1).
• If \(\gamma'(0) = 0\), then proceeding as in Section 2, we obtain \((f \circ \gamma)'(0) = 0\), and again the formula holds.