Chapter 6 My note

6.1 Group

Definition 6.1 (group) A group is an ordered pair ($G\ ,\ \ *)$, where $G$ is a non-empty set and $*$ is a binary operation on $G$ such that the following properties hold:

For all $a,b\ ,c \in G,\ \ \ a*(b*c) = (a*b)*c$ (associative law)
There exists $e \in G$ such that for all $a \in G$, $a*e = e*a = a$ (existence of an identity)
For all $a \in G,\ $ there exists $b \in G$ such that $a*b = e = b*a$ (existence of an inverse)

$b$ is called inverse of $a$ and we write it as $a^{- 1}$ \[a + ( - a) = 0 ~~~~~~~~~~~~~~~~ a\ .\ \frac{1}{a} = 1\]

Example 6.1

$\left( \mathbb{Z,\ +} \right)$, $\left( \mathbb{Q,\ +} \right)$, $\left( \mathbb{R,\ +} \right)$, $\left( \mathbb{C,\ +} \right)$
$\left( \mathbb{Q\backslash}\text{\{}0\},\ \ \cdot \right)$, $\left( \mathbb{R\backslash}\text{\{}0\},\ \ \cdot \right)$, $\left( \mathbb{C\backslash}\text{\{}0\},\ \ \cdot \right)$
$\mathbb{\ Z}^{+}$ with operation + is not a group. Because there is no identity element + in $\mathbb{\ Z}^{+}$.
The set of nonnegative integers (including 0) with operation + is still not a group (no inverse).
$\mathbb{\ Z}^{+}$ with multiplication is not a group (no inverse).
$(M_{m \times n}\left( \mathbb{R} \right),\ + )$ is a group. $m \times n$ matrix with all entries 0 is the identity matrix.

Exercise 6.1

Show that $(\mathbb{Q}^{+},\ *\ )$ is a group, where $a*b = \ \frac{ab}{2}$ for all $a,\ \ b\ \in \mathbb{Q}^{+}$.
Let $U_{n} = \left\{ \theta_{n}^{q}\ |\ \theta_{n} = \cos\left( \frac{2\pi}{n} \right) + i\sin\left( \frac{2\pi}{n} \right);q = 0,\ 1,\ldots,n - 1 \right\}$ where $\theta_{n}^{k} \cdot \theta_{n}^{j} = \theta_{n}^{k + j}$

Verify that ${(U}_{n},\ \ \cdot \ )$ forms a group. $U_{n}$ is the n^th of unity $x^{n} = 1$ in $\mathbb{C}$. Here $U_{1} = \{ 1\}$, $U_{2} = \{ - 1,\ 1\}$, $U_{3} = \{ 1,\ - \frac{1}{2} + \frac{\sqrt{3}}{2}i,\ - \frac{1}{2} - \ \frac{\sqrt{3}}{2}i\}$, $U_{4} = \{ 1,\ \ i,\ - 1,\ - i\}$

Definition 6.2 A group G is said to be [finite group if it has finite number of elements. The number of elements in G is called the [order of G and denoted by $|G|.$

Example 6.2 ${(U}_{n},\ \ \cdot \ )$

Definition 6.3 A group G is said to be [abelian group if $a*b = b*a$ for all $a,\ b \in G$.

Example 6.3 $\mathbb{Z,\ Q,\ R\ }and\mathbb{\ C}$ with usual addition are abelian groups.

$\left( \mathbb{Q\backslash}\text{\{}0\},\ \ \cdot \right)$, $\left( \mathbb{R\backslash}\text{\{}0\},\ \ \cdot \right)$, $\left( \mathbb{C\backslash}\text{\{}0\},\ \ \cdot \right)$

Exercise 6.2 Show that the subset S of $M_{n}\left( \mathbb{R} \right)$ consisting of all invertible $n \times n$ matrices with matrix multiplication is a group but not an abelian group.

Example 6.4 Let $A = \{ 1,\ 2,\ 3\}$

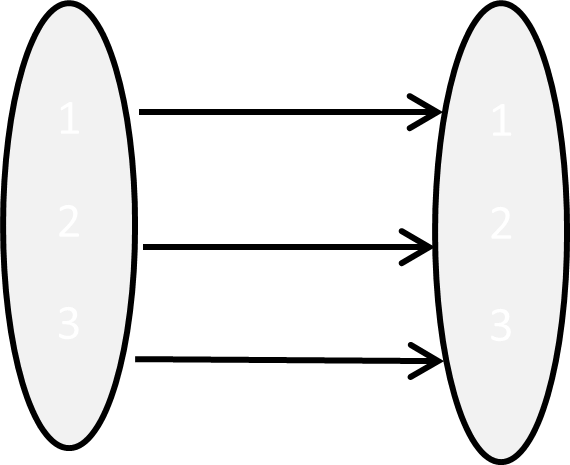	\[\mathbb{i} = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \\ \end{pmatrix}\]
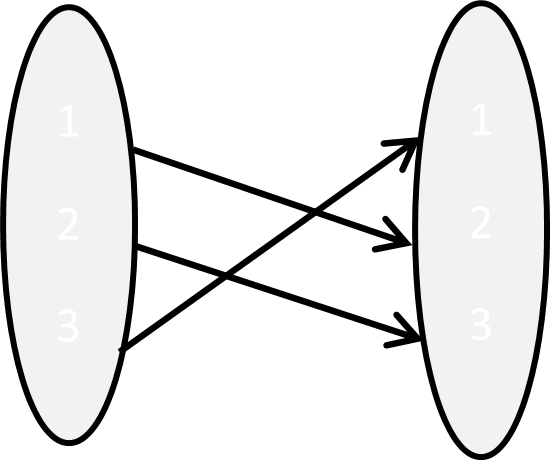	\[\sigma_{1} = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \\ \end{pmatrix}\]
	\[\sigma_{2} = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \\ \end{pmatrix}\]
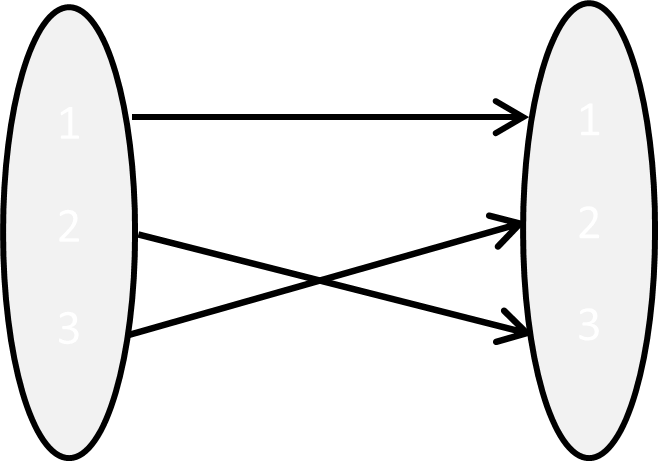	\[\tau_{1} = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \\ \end{pmatrix}\]
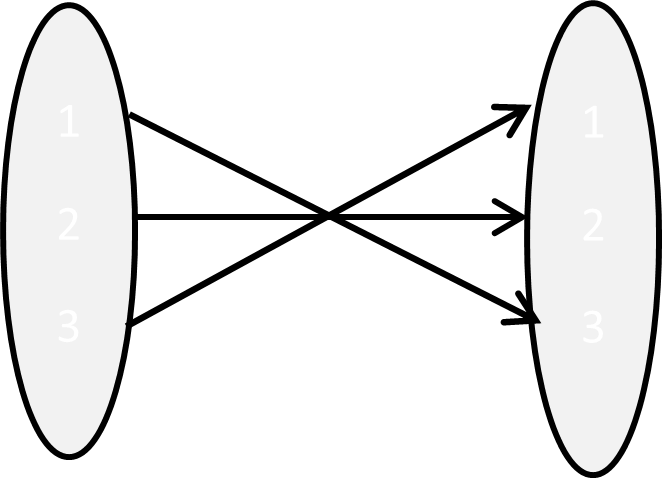	\[\tau_{2} = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \\ \end{pmatrix}\]
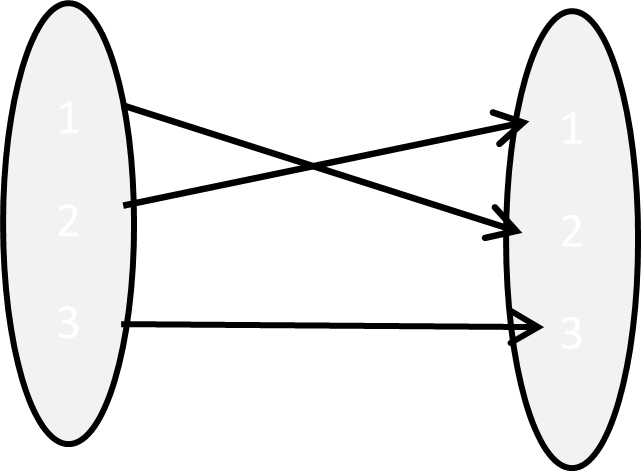	\[ au_3 = \begin{pmatrix} 4 & 5 & 6 \\ 4 & 5 & 6 \\ \end{pmatrix}\]

\[\circ\]	\[i\]	\[\sigma_{1}\]	\[\sigma_{2}\]	\[\tau_{1}\]	\[\tau_{2}\]	\[\tau_{3}\]
\[i\]
\[\sigma_{1}\]
\[\sigma_{2}\]
\[\tau_{1}\]
\[\tau_{2}\]
\[\tau_{3}\]

Lemma 6.1 If ($G\ ,\ \ *)$ is a group, then

Its identity element is unique.
Every $a \in G$ has a unique inverse $a^{- 1} \in G$.
If $a \in G$, $\left( a^{- 1} \right)^{- 1} = a$.
For all $a,\ b \in G$, $(a*b)^{- 1} = b^{- 1}*a^{- 1}$.
$a*b = a*c$ implies $b = c{\ \&\ \ b}*a = c*a$ implies $b = c$ for $a,\ b,\ c\ \in G$.

Proof.

Suppose $e$ and $f$ are identity elements of G.

\[\begin{align} ae &= a = ea\ \ \ \ \forall a \in G\\ af &= a = fa \ \ \ \ \forall a \in G \end{align}\]

Then $ef = f$ as $e$ is an identity and also $ef = e$ as $f$ is an identity. Therefore $e = f$.

Suppose $x$ and $y$ are inverses of $a$ \[\begin{align} xa &= e = ax \ \ \\ ya &= e = a \end{align}\] This gives $x = xe = x(ay) = (xa)y = ey = y$

Hence inverse of $a$ is unique.

If $a \in G$, then $a^{- 1}*a = e = a*a^{- 1}$ and so $a$ is an inverse of $a^{- 1}$. Since the inverse of an element is unique in a group and since $\left( a^{- 1} \right)^{- 1}$ denotes the inverse of $a^{- 1}$, it follows that $\left( a^{- 1} \right)^{- 1} = a$.
\[\begin{align} (ab)\left( b^{- 1}a^{- 1} \right) &= e\\ \left( b^{- 1}a^{- 1} \right)(ab) &= e \end{align}\]

$\therefore(ab)^{- 1} = b^{- 1}a^{- 1}$

Suppose $a*b = a*c$ \[\begin{align} a^{- 1}*a*b &= a^{- 1}*a*c\\ e*b &= e*c\\ b &= c \end{align}\] Similarly, $b*a = c*a \Rightarrow b = c$.

6.2 Subgroup

Definition 6.4 A non-empty subset $H$ of a group $G$ is called a subgroup of $G$ if $H$ itself a group relative to the binary operation in $G$. We shall let $H \subset G$ denotes that $H$ is a subgroup of $G$.

Example 6.5

$\left( \mathbb{Z,\ +} \right) \subset \left( \mathbb{R, +} \right)$
$\left( 2\mathbb{Z,\ +} \right) \subset \left( \mathbb{Z, +} \right)$
$\left( \mathbb{Q,\ \ \cdot} \right) ⊄ \left( \mathbb{R, +} \right)$
Let $G$ be a group $e$ be the identity of $G$ then $\left\{ e \right\} \subset G$

Definition 6.5

If $G$ is a group, then the subgroup consisting of $G$ itself is the improper subgroup of $G$.
All other subgroups are proper subgroups.
The subgroup $\ \left\{ e \right\}$ is the trivial subgroup of $G$. All other subgroups are nontrivial.

Lemma 6.2 A non-empty subset $H$ of a group $G$ is a subgroup if and only if,

$a*\ b \in H$ ($\forall a,b \in H$)
$a^{- 1} \in H$ (for any $a \in H$)

Proof. ($\Rightarrow$) (obvious)

($\Leftarrow$) Suppose we have (i.) and (ii.)

$H$ is non-empty.

$a*(b*c) = (a*b)*c$ ($\forall a,b,\ c \in H$)

Because $a,b,\ c \in G$

By (ii.) for any $a \in H,\ \ a^{- 1} \in H$

Since $a$ and $\ a^{- 1}$ are elements of $\ H$, by (i.) $a*a^{- 1} = e\ \in H$

Hence $H \subset G$.

Remark.

$a*b∈H \forall a,b\in H \Leftrightarrow a^{*}b^{- 1} \in H$
$a^{- 1} \in H$ for any $a \in H \Leftrightarrow a^{*}b^{- 1} \in H$

Proof. Homework

Example 6.6 Let $G$ be a group and $Z(G) = \left\{ b \in G|\ ab = ba\ \ for\ all\ a \in G \right\}$. Show that $Z(G)$ is commutative subgroup of $G$.

Since $ae = a = ea$ for all $a \in G,\ \ e \in Z(G)$ and $Z(G) \neq \phi$.

Let $a,\ b \in Z(G)$.

Then $bc = cb$ for all $c \in G$. \[\begin{align} bc &= cb\\ b^{- 1}bc &= b^{- 1}cb\\ cb^{- 1} &= b^{- 1}cbb^{- 1}\\ cb^{- 1} &= b^{- 1}c \text{ for all } c \in G\\ \end{align}\]

Hence $b^{- 1} \in Z(G)$.

Now $\left( ab^{- 1} \right)c = a\left( b^{- 1}c \right) = a\left( cb^{- 1} \right) = ac\left( b^{- 1} \right) = (ac)b^{- 1} = (ca)b^{- 1} = c\left( ab^{- 1} \right)$ for all $c \in G$.

$\Rightarrow ab^{- 1} \in Z(G)$

Hence $Z(G)\ \subset G$.

By definition $Z(G)$ is commutative.

$Z(G)$ is called the center of $G$.

6.3 Lagrange’s Theorem

Recall

A relation $\sim$ on $S$ called an equivalence relation if it satisfies,

$a \sim a$ for any $a \in S$ (reflexive)
$a\sim b \Rightarrow b\sim a$ (symmetric)
$a\sim b\ \&\ b\sim c \Rightarrow a\sim c$ (transitive)

Example 6.7

Let $n> 1$ be fixed integer. Define on $\mathbb{Z,\ \ }a,b\mathbb{\in Z}$

\[a\sim b \Leftrightarrow \left. \ n \right|a - b\]

where, $\sim$ is an equivalence relation.

This relation is called congruence modulo $n$ and write $a \equiv b\ (mod\ n)$.

Let $G$ be a group and $H$ be a subgroup of $G$. For $a,\ b \in G$ define $a\sim b \Leftrightarrow ab^{- 1} \in H$.

Show that $\sim$ is an equivalence relation.

Definition 6.6 If $\sim$ is an equivalence relation on set $S$ then $\overline{a}$ the class of $a$ is defined by,

$\overline{a} = \left\{ b \in \left. \ S \right|\ b\sim a \right\}$

Example 6.8 Define an equivalence relation on $\mathbb{Z}$ as follows.

$a\sim b \Leftrightarrow 2|a - b$

$\overline{0} = \left\{ y \in \left. \ \mathbb{Z} \right|\ y\sim 0 \right\} = \ \left\{ y\mathbb{\in Z}|\ 2|y \right\} = 2\mathbb{Z}$

$\overline{1} = \left\{ y \in \left. \ \mathbb{Z} \right|\ y\sim 1 \right\} = \left\{ y\mathbb{\in Z}|\ 2|y - 1 \right\} = \left\{ y \in \left. \ \mathbb{Z} \right|y = 2k + 1 \right\} =$ set of all odd integers

$\overline{2} = \left\{ y \in \left. \ \mathbb{Z} \right|\ y\sim 2 \right\} = \left\{ y\mathbb{\in Z}|\ 2|y - 2 \right\} = 2\mathbb{Z}$

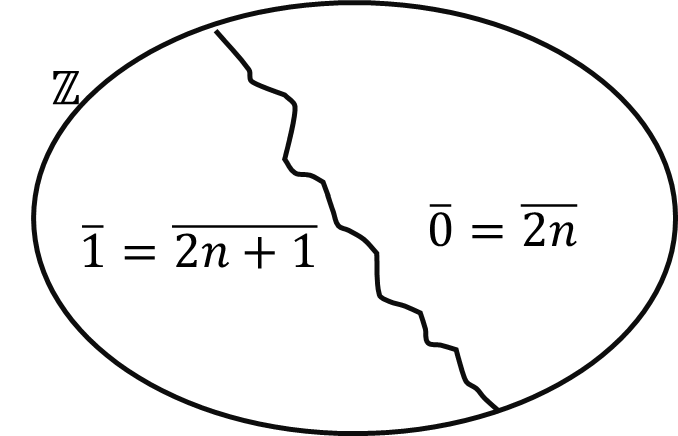
Example 6.9 $G$ be any group and $H$ be a subgroup of $G$. $a\sim b \Leftrightarrow ab^{- 1} \in H$. Find $\overline{a}.$

$\overline{a} = \left\{ ha\ \right|h \in H\} = Ha$

Theorem 6.1 If $\sim$ is an equivalence relation on $S$ then $S = \bigcup\overline{a}$ where the union runs over one element from each class and $\overline{a} \neq \overline{b}$ implies that $\overline{a} \cap \overline{b} = \phi$

Proof. Let $a \in S$. Then $a \in \overline{a} \subseteq \bigcup\overline{a}$. $\Rightarrow S \subseteq \bigcup\overline{a}$ Also, $\bigcup\overline{a\ } \subseteq S$ $\Rightarrow S = \bigcup\overline{a}$ Let $a,b \in S$. Suppose $\overline{a} \cap \overline{b} \neq \phi$. Then there exists $u \in \overline{a} \cap \overline{b}$. Thus $u \in \overline{a}$ and $u \in \overline{b}$. i.e., $u\sim a\ and\ u\sim b$. Since $\sim$ is symmetric $u\sim b$, we have $b\sim u$. Now $b\sim u$ and $u\sim a$ and so transitivity of $\sim$, $b\sim a$. This implies that $b \in \overline{a}$. Hence $\overline{a} = \overline{b}$.

Theorem 6.2 (Lagrange's Theorem) If $G$ is a finite group and $H$ is a subgroup of $G$, then order of $H$ divides order of $G$.

Theorem 6.3 If $G$ is a group of prime order then $G$ has only trivial subgroups $\left\{ e \right\}$ and $G$.

Proof. $|G| = p$ – prime

Let $H \subset G$, then

$|H|=1 \Rightarrow H=\left\{ \mathbb{e} \right\}$
$|H|=p \Rightarrow H=G$

Exercise 6.3 Let $n> 1$ be a fixed integer. $a,b\mathbb{\in Z}$. Define \[a\sim b \Leftrightarrow n|a - b \Leftrightarrow a - b \in n\mathbb{Z\ }\]

Find $\overline{a}$.
Show $\overline{0,}\ \overline{1},\ \ .\ .\ .,\ \overline{n - 1}$ are disjoint and $\mathbb{Z =}\overline{0}\ \cup \overline{1} \cup .\ .\ .\ \cup \overline{n - 1}$.
Let $\mathbb{Z}_{n} = \left\{ \overline{0,}\ \overline{1},\ \ .\ .\ .,\ \overline{n - 1} \right\}$. Show that $\mathbb{Z}_{n}$ forms a group under the binary operation

\[\overline{x} + \overline{y} = \overline{x + y}\].

Let $\overline{a},\ \overline{b},\ \overline{c},\ \overline{d} \in \mathbb{Z}_{n}$. Suppose $\overline{a} = \overline{c}$ and $\overline{b} = \overline{d}$.

Then $n|a - c\ and\ n|b - d$.

i.e., $\exists\ s\ and\ t$ such that $ns = {a - c}$ and ${nt} = b - d$

hence $n(s + t) = (a + b) - (c + d)$ and

$\left. \ n \right|(a + b) - (c + d)$

$\Rightarrow \overline{a + b} = \overline{c + d}$

Hence + is well defined.

Since $\left( \overline{a} + \overline{b} \right) + \overline{c} = \overline{a} + \left( \overline{b} + \overline{c} \right)$, + is associative.

Now $\overline{0} \in \mathbb{Z}_{n}$ and for all $\overline{a} \in \mathbb{Z}_{n}$

$\overline{a} + \overline{0} = \overline{a + 0} = \overline{a} = \overline{0 + a} = \overline{0} + \overline{a}$

This shows that $\overline{0}$ is the identity element.

Also, for all $\overline{a} \in \mathbb{Z}_{n}$, $\overline{- a} \in \mathbb{Z}_{n}$ and

$\overline{a} + \overline{- a} = (\overline{a + - a)} = \overline{0} = (\overline{- a + a)} = \overline{- a} + \overline{a}$

Thus $\overline{- a}$ is the inverse of $\overline{a}$.

Hence ($\mathbb{Z}_{n},\ +$) is a group.

Is it commutative?

Yes, $\overline{a} + \overline{b} = \overline{a + b} = \overline{b + a} = \overline{b} + \overline{a}$

Define multiplication in $\mathbb{Z}_{n}$ as

$\overline{a}.\overline{b} = \overline{a.b}$

Let $\overline{a},\ \overline{b},\ \overline{c},\ \overline{d} \in \mathbb{Z}_{n}$. Suppose $\overline{a} = \overline{c}$ and $\overline{b} = \overline{d}$

Then $n|a - c\ and\ n|b - d$

i.e., $\exists\ s\ and\ t$ such that $ns = {a - c\ and}{nt} = b - d$ \[\begin{align} a = ns + c \tag{6.1} \\ b = nt + d \tag{6.2} \end{align}\]

By (6.1) and (6.2),

$a\cdot b = (ns + c)\left( {nt}{+ d} \right) = n^{2}st + nsd + ntc + c\cdot d$

$a\cdot b = n\cdot k + c\cdot d$

$n\cdot k = a \cdot b - c\cdot d$

$\Rightarrow {n\ |\ a\cdot b} - c \cdot d$

$\Rightarrow \overline{a \cdot b} = \overline{c \cdot d}$

Hence $.$ is well defined.

Since $\left( \overline{a}\cdot \overline{b} \right)\cdot \overline{c} = \overline{a} \cdot \left( \overline{b} \cdot \overline{c} \right)$, $\cdot$ is associative.

Now $\overline{1} \in \mathbb{Z}_{n}$ and for all $\overline{a} \in \mathbb{Z}_{n}$

$\overline{a} \cdot \overline{1} = \overline{a.1} = \overline{a} = \overline{1 \cdot a} = \overline{1} \cdot \overline{a}$

This implies that $\overline{1}$ is the identity element.

Does $\overline{a}$ has an inverse in $\mathbb{Z}_{n}$ for any $\overline{a} \in \mathbb{Z}_{n}$?

No.

If $\overline{a} \in \mathbb{Z}_{n}$ and $\overline{a} \neq \overline{0}$, then $\overline{a}$ has an inverse if and only if gcd($a,n$) = 1.

Proof. Let $\overline{a} \in \mathbb{Z}_{n}$ and $\overline{a} \neq \overline{0}$. Suppose gcd($a,n$) = 1.

Then there exists $b,r\mathbb{\in Z}$ such that $ab + nr = 1$.

$\Rightarrow ab - 1 = - nr$

This implies that $\overline{ab} = \overline{1}$ or $\overline{a}.\overline{b} = \ \overline{1}$

Since $ab = ba$, $\overline{b}.\overline{a} = \overline{ba} = \overline{ab} = \ \overline{1}$

Thus $\exists\overline{b} \in \mathbb{Z}_{n}$ such that $\overline{a}.\overline{b} = \ \overline{1} = \ \overline{b}.\overline{a}$ and so $\overline{a}$ has an inverse.

Conversely suppose $\overline{a} \in \mathbb{Z}_{n}$, $\overline{a} \neq \overline{0}$ and $\overline{a}$ has an inverse.

Then there exists $\overline{b} \in \mathbb{Z}_{n}$ such that $\overline{a}\cdot \overline{b} = \overline{1}$.

This implies that $n\ |\ ab - 1$

Hence $ab - 1 = nr$ for some $r\mathbb{\in Z}$.

Thus $ab - nr = 1,\ \ \gcd(a,n) = 1$.

Let $U_{n}$ be the set of all elements of $\mathbb{Z}_{n} \smallsetminus \left\{ \overline{0} \right\}$ that have an inverse in $\mathbb{Z}_{n} \smallsetminus \left\{ \overline{0} \right\}$.

i.e., $U_{n} = \left\{ \overline{a} \in \mathbb{Z}_{n} \smallsetminus \left. \ \left\{ \overline{0} \right\} \right|\gcd(a,n) = 1 \right\}$

Then $(U_{n},\ \ \cdot )$ is a group.

Example 6.10 If $n = 6$,

$\mathbb{Z}_{6} = \left\{ \overline{0},\overline{1},\ \overline{2},\overline{3},\overline{4},\overline{5}\}\ \ \ \ \right.\ $

$U_{6} = \left\{ \overline{1,}\ \overline{5} \right\}$

$U_{8} = \left\{ \overline{1},\overline{3},\overline{5},\ \overline{7} \right\}$

$U_{7} = \left\{ \overline{1},\overline{2},\overline{3},\overline{4,}\overline{5},\ \overline{6} \right\}$

Let ($G,\ \ *$) be a group, $a \in G$ and $n\mathbb{\in Z}$. We now define the integral power $a^{n}$ of $a$ as follows.

\[\begin{align} a^{0} &= \mathbb{e}\\ a^{n} &= a*a^{n - 1} \text{ if } n 0\\ a^{n} &= \left( a^{- 1} \right)^{- n} \text{ if } n < 0 \end{align}\]

Note that $a^{n} = \left( a^{- n} \right)^{- 1}$ if $n < 0$.

Definition 6.7 Let ($G,\ \ *$) be a group and $a \in G$. If there exists a positive integer $n$ such that $a^{n} = \mathbb{e}$, then the smallest such positive integer is called the [order] of $a$. If no such positive integer $n$ exists, then we say that $a$ is of infinite order. We denote the order of an element $a$ by $O(a)$.

Example 6.11 Consider $\left( \mathbb{Z}_{6},\ + \right)$, $\mathbb{Z}_{6}$ has order 6.

$\overline{0,}\overline{1},\ \overline{2,}\overline{3},\overline{4,}\overline{5}$ have orders 1, 6, 3, 2, 3, 6 respectively.

${\overline{3}}^{2} = \overline{3} + \overline{3} = \overline{6} = \overline{0}$ and 2 is the smallest positive $n$ such that ${\overline{3}}^{n} = \overline{0}$.

Theorem 6.4 Let ($G,\ \ *$) be a group and $a$ be an element of $G$ such that $O(a) = n.$

If $a^{m} = \mathbb{e}$ for some positive integer $m$, then $n$ divides $m$.
For every positive integer $t$, $0\left( a^{t} \right) = \frac{n}{\gcd(t,n)}$

Proof.

By the division algorithm, $\exists q,\ r\mathbb{\in Z}$ such that $m = nq + r\ \ \ 0 \leq r < n$. Now $a^{r} = a^{m - nq} = a^{m}.a{- nq} = .( a^{n} )^{- q} = .^{- q} = . Since $n$ is the smallest positive integer such that $a^{n} = \mathbb{e}$ and $a^{r} = \mathbb{e}$, it follows that $r = 0$. Thus $m = nq$. This implies that $n$ divides $m$.
Let $0\left( a^{t} \right) = k$. Then $a^{tk} = e.$ By (i.) $n$ divides $kt$. Thus $\exists r\mathbb{\in Z}$ such that $kt = nr$. Let $\gcd(t,n) = d$. Then $\exists u,v\mathbb{\in Z}$ such that $t = du,\ \ n = \mathbb{d}v$ and $\gcd(u,v) = 1$ Now $kt = nr \Rightarrow k\mathbb{d}u = dvr$ $\Rightarrow {ku} = rv$ Thus $v$ divides $ku$. Since $\gcd(u,v) = 1$, $v$ divides $k$. Thus $\frac{n}{d}$ divides $k$. Now $\left( a^{t} \right)^{\frac{n}{d}} = a^{\frac{nt}{d}} = a^{\frac{n\mathbb{d}u}{d}} = a^{nu} = \left( a^{n} \right)^{u} = \mathbb{e}^{u} = \mathbb{e}$. Since $0\left( a^{t} \right)^{k} = k$, $k$ divides $\frac{n}{d}$. Since $k$ and $\frac{n}{d}$ are positive integers, $k = \ \frac{n}{d}$ Hence $0\left( a^{t} \right) = k = \frac{n}{d} = \frac{n}{\gcd(t,n)}$.

Lemma 6.3 Let $G$ be a group. If $a \in G$ and $O(a) = m,$ then $A = \left\{ \mathbb{e},a,a^{2},\ .\ .\ .,a^{m - 1}\ \right\}$ is a subgroup of $G$.

Proof. HW

Theorem 6.5 Let $G$ be a finite group. Then $O(a)|\ |G|.$

Proof. Let $O(a) = m$

Take $A = \left\{ \mathbb{e},a,a^{2},\ .\ .\ .,a^{m - 1}\ \right\}$ We have seen that $A \subset G$ and $|A| = m = O(a)$ By Lagrange’s theorem, $|A|\ |\ |G| \Rightarrow O\left. \ (a) \right|\ |G|$ Since $O\left. \ (a) \right|\ |G|$, we have $n = |G| = kO(a)$ $a^{n} = a^{kO(a)} = \left( a^{O(a)} \right)^{k} = \mathbb{e}^{k} = \mathbb{e}$ Hence we have proved that if $G$ is a finite group of order $n,\ then\ a^{n} = \mathbb{e}$ for any $a \in G$. Hence the order of any element of a finite group is finite.

6.4 Group Homorphism

Definition 6.8 Let $(G, *)$ and $(G_1, *_1)$ be groups, and let $f$ be a function from $G$ into $G_1$. Then $f$ is called a homomorphism of $G$ into $G_1$ if for all $a, b \in G$, \[ f(a * b) = f(a) *_1 f(b) \]

Example 6.12

$f: (R^+, \cdot) \to (R, +)$, where $f(x) = \log_{10}(x)$:
For $x, y \in R^+$,
\[ f(x \cdot y) = \log_{10}(xy) = \log_{10}(x) + \log_{10}(y) = f(x) + f(y) \]
Therefore, $f$ is a homomorphism.
Let $G$ be an abelian group. Define $f: G \to G$ by $f(a) = a^2 = a \cdot a, \, a \in G$:
For $a, b \in G$,
\[ f(a * b) = (a * b)^2 = a * b * a * b = a^2 * b^2 = f(a) * f(b) \]
Hence, $f$ is a homomorphism.
Let $G, G_1$ be any groups. Define $f: G \to G_1$ by $f(a) = e_1$ for all $a \in G$, where $e_1$ is the identity of $G_1$:
Since $f(a * b) = e_1 = e_1 *_1 e_1 = f(a) *_1 f(b)$ for all $a, b \in G$, $f$ is a homomorphism.

For any groups $G$ and $G_1$, there is always at least one homomorphism $f: G \to G_1$, namely the trivial homomorphism defined by $f(a) = e_1$ for all $a \in G$, where $e_1$ is the identity of $G_1$.

Exercise 6.4 Show that the identity map is a homomorphism.

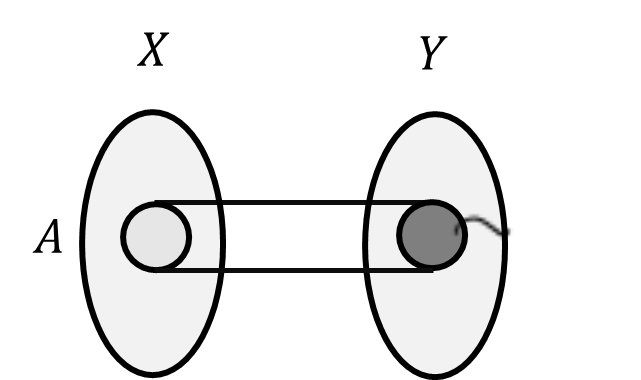
Definition 6.9 Let $\phi$ be a mapping of a set $X$ onto a set $Y$, and let $A \subseteq X$ and $B \subseteq Y$. The image $\phi[A]$ of $A$ in $Y$ under $\phi$ is
\[ \phi[A] = \{\phi(a) \mid a \in A\} \]
The set $\phi[X]$ is sometimes called the range of $\phi$. The inverse image $\phi^{-1}[B]$ of $B$ in $X$ is
\[ \phi^{-1}[B] = \{x \in X \mid \phi(x) \in B\} \]

Exercise 6.5 If $f: G \to G'$ is a group homomorphism, then $\text{Im} \, f = f[G]$ is a subgroup of $G'$.

Theorem 6.6 Let $\phi$ be a homomorphism of a group $G$ into a group $G'$.
1. If $e$ is the identity in $G$, then $\phi(e)$ is the identity $e'$ in $G'$.
2. If $a \in G$, then $\phi(a^{-1}) = (\phi(a))^{-1}$.
3. If $H$ is a subgroup of $G$, then $\phi(H)$ is a subgroup of $G'$.
4. If $K'$ is a subgroup of $G'$, then $\phi^{-1}[K']$ is a subgroup of $G$.

Definition 6.10 Let $G$ and $G_1$ be groups. A homomorphism $f: G \to G_1$ is called:
- An epimorphism if $f$ is onto $G_1$.
- A monomorphism if $f$ is one-to-one.
- An isomorphism if $f$ is both one-to-one and onto $G_1$. In this case, we write $G \cong G_1$ and say that $G$ and $G_1$ are isomorphic.
- An automorphism if $f$ is an isomorphism of a group $G$ onto itself.

Theorem 6.7 Let $f$ be an isomorphism of a group $G$ onto $G_1$. Then:
1. $f^{-1}: G_1 \to G$ is an isomorphism.
2. For all $a \in G$, $O(a) = O(f(a))$.
3. $G$ is commutative if and only if $G_1$ is commutative.
4. $G$ is cyclic if and only if $G_1$ is cyclic.

Proof. Homework.

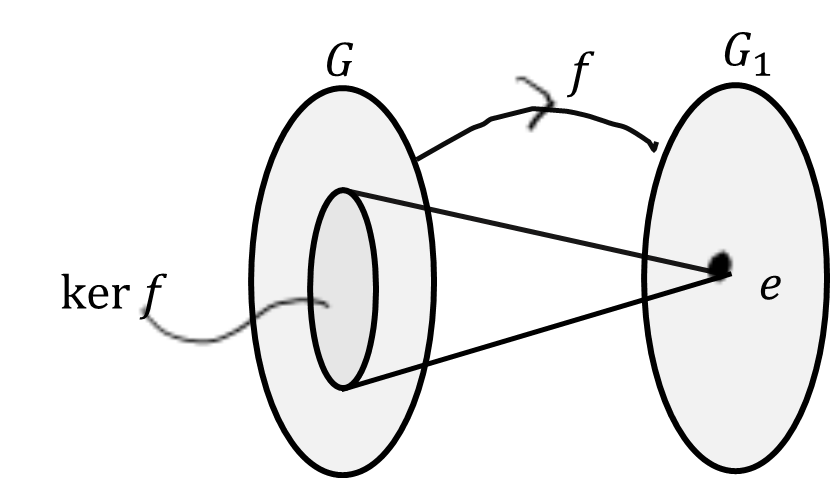
Definition 6.11 If $f: G \to G_1$ is a homomorphism, the kernel of $f$ is defined by:
\[ \ker f = \{g \in G \mid f(g) = e_{G_1}\} \]

Example 6.13 Define $f: (\mathbb{Z}, +) \to (\mathbb{Z}_n, +)$ by $f(a) = \bar{a}$.
For $a, b \in \mathbb{Z}$:
\[ f(a + b) = \overline{a + b} = \bar{a} +_n \bar{b} = f(a) +_n f(b) \]
Thus, $f$ is a homomorphism.

\[ \ker f = \{a \in \mathbb{Z} \mid f(a) = \bar{0}\} = \{a \in \mathbb{Z} \mid a \text{ is divisible by } n\} = \{qn \mid q \in \mathbb{Z}\} \]

Theorem 6.8 Let $f$ be a homomorphism of a group $G$ into a group $G_1$. Then $f$ is one-to-one if and only if $\ker f = \{e\}$.

Proof.

Suppose $f$ is one-to-one. Let $a \in \ker f$. Then $f(a) = e_1 = f(e)$. Since $f$ is one-to-one, $a = e$. Thus, $\ker f = \{e\}$.
Conversely, suppose $\ker f = \{e\}$. Let $a, b \in G$ and suppose $f(a) = f(b)$. Then:
\[ f(ab^{-1}) = f(a)f(b^{-1}) = f(a)f(b)^{-1} = e_1 \]
Thus, $ab^{-1} \in \ker f = \{e\}$, so $ab^{-1} = e$, and $a = b$.

Theorem 6.9 Let $f$ be a homomorphism of a group $G$ into a group $G_1$. Then $\ker f$ is a subgroup of $G$.

Proof. Homework.